Estequiometria: Gases
Produzido por Juliana EcheniqueTeoria
Fala aí! Bem vindo ao RespondeAí! Bora aprender sobre a estequiometria em reações gasosas?!
Mas afinal, qual é a diferença na estequiometria dos gases?
Pra a gente começar a entender, se liga na reação de síntese de amônia na imagem abaixo:
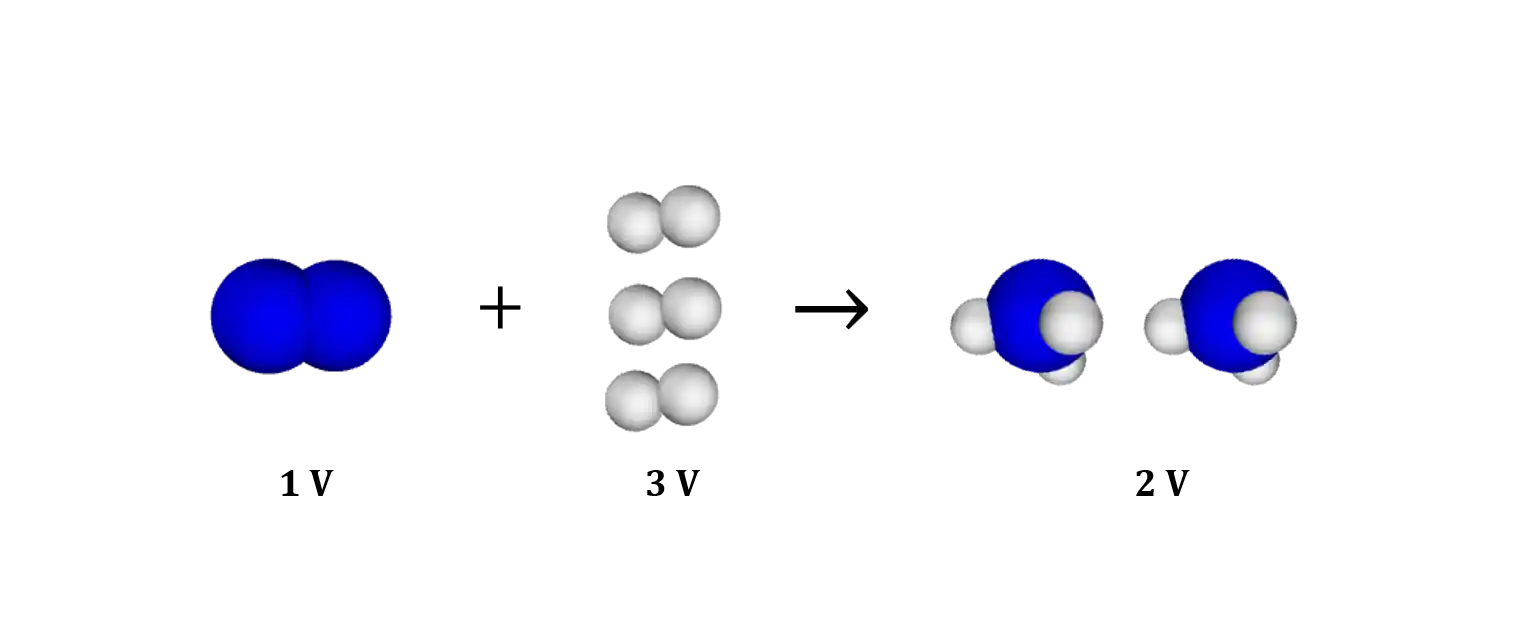
Em qualquer reação química o princípio de conservação de massa é obedecido. Isso é, a massa inicial é igual a massa final. Em reações envolvendo sólidos e líquidos a conservação de volume também é obedecida, então, o
Mas isso muitas vezes não é verdade nas reações gasosas! No exemplo da imagem a cima o
-Então como incluir essa variação de volume nas nossas contas?
É o que vamos aprender hoje!
Lei dos gases ideais
Uma das estrelas desse tópico é a lei dos gases ideais, ou equação de Clapeyron, nossa velha conhecida de guerra:
Gases ideais são gases que obedecem essa relação sob todas as condições.
Onde
Ela vai ser muito útil principalmente quando estivermos lidando com gases fora da CNPT!
Exemplo: Estequiometria dos Gases fora da CNPT
A reação abaixo é a reação dos airbags dos carros:
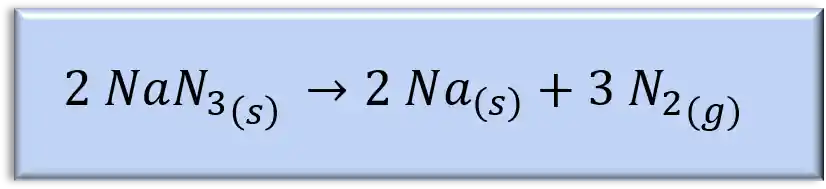
O
Beleza, então queremos saber a massa de
Esses dados são referentes a condição no nitrogênio. Então podemos usar a Lei dos gases ideais pra achar o seu número de mols!
Isolamos o
Podemos usar
Achamos o número de mols de
Ficamos então com:
Pra finalizar achamos a massa, sabendo que
Aeee!!
Se você achou esse exemplo tranquilo, eu tenho uma boa notícia! Quando os gases estão na CNTP tudo fica muito mais fácil!
Exemplo: Estequiometria dos Gases na CNTP
As CNTP são as condições normais de temperatura e pressão, definidas à
Nas CNTP, o volume molar de um gás é
Essa regrinha vem do Princípio de Avogadro, que diz que nas mesmas condições de temperatura e pressão, um mol de gás ocupa o mesmo volume, independente da sua identidade química. Ou seja, tanto faz se o gás for
Vamos considerar a seguinte reação:
Qual a massa de
Sabemos que com
Como a relação entre o
Como a massa molar do
Densidade dos gases
A densidade é sempre calculada por:
A partir da lei dos gases ideais, conseguimos escrever:
Podemos usar essa relação, para gases ideais, sempre que a questão envolver densidade!
Mistura de gases
E quando a reação é entre vários gases? Ou entre uma mistura de gases e um sólido? Como a gente relaciona eles?
A gente pode fazer relacionando mol – mol, como com os compostos sólidos e líquidos, mas existe um conceito que pode ajudar, o conceito de pressão parcial.
A pressão parcial de um gás em uma mistura de gases é a pressão que esse gás exerceria se ele estivesse sozinho no recipiente! Ou seja, se eu tiver uma mistura de e de pressão total
Outro método de expressar a pressão parcial, é através da fração molar
E para uma mistura de A, B, C...
Agora, depois desses resumão, que tal conferir nosso conteúdo em vídeo?
A dica para ficar craque em estequiometria em geral é praticar muiiiiito! Então vamos fazer uns exercícios? 😊
Densidade dos gases
Mistura de gases
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 166-Exercício 4.53
O processo de Haber de síntese da amônia é um dos processos industriais mais importantes para o bem-estar da humanidade. Ele é muito usado na produção de fertilizantes, polímeros e outros produtos. Sua reação é:
a) Que volume de hidrogênio em e deve ser usado para produzir tonelada de
b) Que volume de hidrogênio seria necessário em (a) se o gás fosse fornecido em 376 atm e
Passo 1
a) Da reação química a gente tira a relação estequiométrica entre o e o em mol, porém queremos comparar volume de e massa de né?
Para ficar mais fácil, vamos passar o que a gente tem pra mol! Queremos produzir 1 tonelada (de que tem massa molar 17g.
Ou seja, precisamos produzir 58823,53 mols de . E precisamos descobrir quantos mols de precisamos usar pra isso!
Da reação:
Dos dados do problema:
Passo 2
Ok, agora precisamos transformar esse número de mols em volume, que é o que o problema pede. Para isso, basta usar a lei dos gases ideais 😊
Como o enunciado quer que seja a , então . Já a temperatura tem que ser . Jogando os dados
Passo 3
b) Se trocarmos as condições que o gás é fornecido, só mudamos o passo 2, já que o número de mols segue o mesmo!
Então precisamos só refazer o cálculo com a lei dos gases ideais usando os novos paramêtros:
Agora o enunciado quer que seja a , então . Já a temperatura tem que ser . Jogando os dados
Faz sentido acharmos menos litros do que em (a), já que a pressão e o volume são grandezas inversamente proporcionais! Ou seja, quanto maior a pressão, menor o volume e vice-versa 😊
Resposta
a)
b)
Exercício Resolvido #2
Adaptada de BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício Como Fazer 10.4
O carbonato de cálcio, , decompõe-se com aquecimento para produzir e . Uma amostra de é decomposta e o dióxido de carbono é coletado em um frasco de 250 ml. Depois de a decomposição se completar, o gás tem pressão de 1,3 atm à temperatura de . Qual a quantidade de matéria de gás produzida? Qual a massa da amostra de ?
Passo 1
Para saber quantos mols de foram formados, basta a gente aplicar a lei dos gases ideais, já que queremos e já temos a pressão, a temperatura e o volume...
Passo 2
Já para a segunda pergunta, precisamos montar a equação, já que precisamos saber a relação entre o e o 😊
Nesse caso o enunciado já dá a equação e ela tem proporção 1:1:1, ou seja, ela já está balanceada! Mas é sempre bom verificar o balanceamento antes de fazer os cálculos estequiométricos, ein?
Da reação, temos:
Dos dados do problema:
A amostra tem, portanto, 0,013 mol de , que tem massa molar de .
Resposta
É produzido 0,013 mol de e a amostra tem .
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 166-Exercício 4.55
Que condição inicial produziria o maior volume de dióxido de carbono na combustão de com excesso de gás oxigênio para produzir dióxido de carbono e água:
a) 2 L de ;
b) 2 g de ?
O sistema é mantido na temperatura de e 1 atm.
Passo 1
Como qualquer combustão, a reação vai ser a fonte de carbono + gerando e . No caso do , a reação é:
Ou seja, quanto mais mols de envolvidos, maior o volume de gerado (já que mais mols vão ser formados!).
Então, precisamos comparar os números de mols encontrados em (a) e em (b) e ver qual dos dois é maior.
a) Temos volume, temperatura e pressão: só usar a lei dos gases ideais!
b) A massa molar do é 16g, e, portanto:
Portanto, a opção b tem mais mols de e gera mais e 😊
Resposta
A letra b.
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 166-Exercício 4.57
O dióxido de carbono e a água produzem, por meio de uma série de etapas enzimáticas do processo de fotossíntese, glicose e oxigênio, de acordo com a equação:
Sabendo-se que a pressão parcial do dióxido de carbono na troposfera é e que a temperatura é , calcule o volume de ar necessário para produzir 10g de glicose.
Dado: a pressão do ar na troposfera é a pressão atmosférica (1 atm).
Passo 1
Vamos com calma que esse exercício tem uns dados meio difíceis de manipular! Ok, ele diz que queremos 10g de glicose e precisamos saber a quantidade de ar para produzir isso. Mas não tem ar na reação química, certo?
O que tem é o , que está presente no ar com uma pressão parcial de Ou seja, precisamos primeiro calcular quanto de precisamos para produzir 10g de glicose para, a partir dele, calcular o volume de ar!
Então vambora!
A relação molar é dada pela equação química, e a massa molar da glicose é .
Ou seja, para produzirmos 10g de glicose, precisamos de 0,334 mols de .
Passo 2
Ok, esse passo agora é mais difícil porque a relação não é nem um pouco óbvia... Sabemos que a pressão do ar na atmosfera é .
Ou seja, a pressão total é . Com a pressão parcial e a fração molar, conseguimos calcular o número de mols de ar necessário, já que .
Como
Agora é só calcular isso em litros!
Resposta
Exercício Resolvido #5
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício Como Fazer 10.11
Um estudo dos efeitos de certos gases no crescimento de plantas requer uma atmosfera sintética composta de mol de , mol de e de Ar.
a) Calcule a pressão parcial de na mistura se a pressão atmosférica total for 745 Torr.
b) Se a atmosfera é para ser mantida em um espaço de 120L a 295K, qual é a quantidade de matéria de necessária?
Passo 1
a) Para calcular a pressão parcial de , é só a gente usar a definição, já que o enunciado dá pra gente a fração molar (18% em mol de ):
Passo 2
b) A atmosfera inclui todos os gases, inclusive o ... Então, usando a lei dos gases ideais, conseguimos calcular o número total de mols, com o incluso!
Como a porcentagem de é 18% em mol do número total de mols, ela vai correponder a:
Resposta
a) 134,1 Torr
b) 0,875 mols de
Exercício Resolvido #6
Adaptado de Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 166-Exercício 4.54
A nitroglicerina é um líquido sensível ao choque, que detona pela reação
Calcule o volume total de gases produzido, em 215 kPa e , na detonação de 454g de nitroglicerina. Qual a fração molar do e do
Passo 1
Para cada 4 mols de glicerina que reagem, produzimos 29 mols de gases em geral. Assim, se reagirmos 454g de nitroglicerina, de massa molar 227g/mol:
Ou seja,
Quando a gente coloca na lei dos gases ideais...
Ou seja, o volume total de gases produzido é 307,4 L.
Passo 2
Para calcular a fração molar de e temos que pensar na definição de fração molar:
No caso desse problema, o é 58 mols, o número de mol de todos os gases formados. Assim, é só a gente usar a proporção entre nitroglicerina e cada um dos gases (dada pela equação balanceada) para calcular o de cada gás!
- No caso do
- No caso do
Dado da equação:
Dado do problema:
Logo, a fração molar do é:
Dado da equação:
Dado do problema:
Logo, a fração molar do é:
Resposta
O volume é 307,4 L, e
Exercício Resolvido #7
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed. Prentice-Hall, 2005, Exercício 10.89
Suponha que um cilindro de motor de automóvel tenha volume de .
a) Se o cilindro está cheio de ar a e 0,980 atm, qual a quantidade de matéria de presente?
b) Quantos gramas de poderiam ser queimados por essa quantidade de , supondo a combustão completa com formação de e água?
Dado: A fração molar de no ar é 21%.
Passo 1
a) Para descobrirmos o número de mol de basta usarmos o dado da fração molar de no ar e a lei dos gases ideais!
Temos p, V, R e T, e, a partir disso, conseguimos calcular a quantidade de mols de ar dentro do motor, já que o volume é ocupado por tooodo o ar, não só o oxigênio. Depois, com esse número de mols, calculamos a quantidade de mols de à partir da fração molar. Vamos lá 😊
A fração molar do é definida por:
Passo 2
b) A reação de combustão do é:
Ou seja, a proporção octano - é 1 mol octano para 12,5 mols de . Se temos ...
Como a massa molar do octano é 114g,
Resposta
a)
b)
Exercício Resolvido #8
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 374-Exercício 9.23
O pentafluoreto de iodo gasoso, , pode ser preparado pela reação de iodo sólido e flúor gasoso:
Adicionam-se a um frasco de 5L contendo 10g de , 10g de e a reação prossegue até que um dos reagentes seja completamente consumido. Depois de a reação se completar, a temperatura no frasco é .
a) Qual a pressão parcial de no frasco?
b) Qual a fração em quantidade de matéria de no frasco?
Passo 1
Para calcularmos a pressão parcial de , precisamos ver o que acontece na reação!
Temos, de início, 10g de . Como a proporção da equação é molar, vamos passar isso para mols:
E adicionamos 10g de
Como a proporção é 1 mol de 5 mols de , para reagir com 0,04 mols de precisamos de 0,26 mols de O que significa que temos um excesso de 0,14 mol de
Ou seja, o número de mols total no final da reação vai ser:
Com esse número, podemos calcular as frações molares de cada componente! (e já respondemos a letra b!)
Passo 2
Agora, para calcularmos a pressão parcial de cada componente, precisamos da pressão total, já que a pressão parcial é calculada por:
Assim...
Obs: um outro jeito de fazer era calcular com o n de cada gás! Assim, eu já acharia a pressão parcial direto, sem ter que calcular a fração molar 😊
Calculando as pressões parciais...
Resposta
a) 0,92 atm.
b) 0,36 ou 36%.
Exercício Resolvido #9
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 166-Exercício 4.65
Um balão de 1L contém o gás nitrogênio, em , em 0.5 bar. 0,10 mol de é adicionado ao balão e os gases se misturam. Em seguida, uma torneira se abre para permitir a saída de 0,020 mol de moléculas. Qual é a pressão parcial do oxigênio na mistura final?
Passo 1
Ok, vamos devagar que essa é difícil!
Temos uma mistura inicial de e, à essa mistura, vamos adicionar As condições da mistura gasosa são:
Para calcular temos que usar a lei dos gases ideais com as condições iniciais do balão com
Assim, o número de mols total na mistura é 0,121 mols. A fração molar de cada componente é:
Passo 2
Quando a torneira se abre e parte da mistura escapa, a gente considera que as frações molares vão se manter, o que vai mudar é só a quantidade de mols final, e, consequentemente, a pressão dentro do balão...
Agora, com as frações molares, a gente pode calcular a pressão parcial do oxigênio!
Resposta
1,96 atm.
Exercício Resolvido #10
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp 168-Exercício 4.105
Um balão de volume 5L foi evacuado e 43,78g de tetróxido de dinitrogênio () foram admitidos. Em , este composto é um sólido incolor. A amostra foi aquecida até e, no processo, se vaporiza e se dissocia parcialmente para formar o gás . A pressão cresce lentamente e se estabiliza em 2,96 atm.
a) Escreva uma equação para a reação.
b) Se o gás que está no frasco em fosse exclusivamente , qual seria a pressão?
c) Se todo o gás que está no frasco fosse qual seria a pressão?
d) Quais são as frações molares de e quando a pressão se estabiliza em 2,96 atm?
Passo 1
a)
Passo 2
b) Como temos 43,78g de , que tem uma massa molar de 92g:
Passo 3
c) Se a dissociação for completa, obteremos (já que a proporção é 1:2 entre .
Passo 4
d) Quando a pressão se estabiliza em 2,96 atm, temos um número total de mols gasosos que pode ser calculado por:
Se começamos com 0,476 mols de , e temos um de 0,605 mols no final...
Onde é a quantidade de que dissociou!
Isso quer dizer que, na reação, foi formado 0,26 mols de e 0,12 mols de dissociaram.
No final, então, vamos ter e .
As frações molares vão ser:
Resposta
a)
b) 2,326 atm
c) 4,652 atm
d)