Cálculos de pH
Teoria
Ácidos e Bases Fortes
Aqui não tem muito mistério, a gente já vem fazendo esse tipo de cálculo de pH.
Para ácidos e bases fortes, consideramos ionização total.
Assim, a concentração de no meio é exatamente igual a concentração analítica do ácido, . Ou seja, a quantidade adicionada no meio.
Da mesma forma, a concentração de é exatamente igual a concentração analítica da base, , porque toda base “vira” mais um cátion.
Quando temos mistura de ácidos e bases fortes, consideramos que eles se neutralizam entre si e o excesso de ou no meio é quem define o pH.
Olha aí:
Se a gente misturar 3,0 mL de uma solução de M com 2,0 mL de uma solução de M, qual o pH resultante?
A gente tem que ver quantos mols (número de mols) de e quantos mols de estão sendo misturados.
Como , esses caras vão se neutralizar até consumir todo o (em menor quantidade) e o excesso de vai definir o pH do meio.
O que sobra de após a neutralização será:
E qual será a concentração de ?
Pra isso a gente vai dividir o número de mols de pelo volume final da solução, que é 5 mL (2,0 mL + 3,0 mL):
Ácidos e Bases Fracas
Já calculamos o pH de ácidos ou bases fracas.
Mas agora vamos “sistematizar” isso ai. Pra passar menos trabalho.
Vamos fazer todo o estudo para um ácido fraco e depois “estender” os resultados para bases também ok?
A gente sabe que nem todo o ácido fraco colocado em solução vira/produz . Então, nesse caso, .
Até agora, pra calcular pH de ácido fraco, a gente usa aquela tabela do equilíbrio.
Pra calcular o pH de uma solução de ácido acético de, , faríamos:
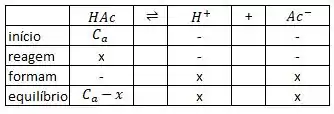
E a gente era obrigado a resolver uma equação de 2° grau...
Generalizando:
Fazendo as contas:
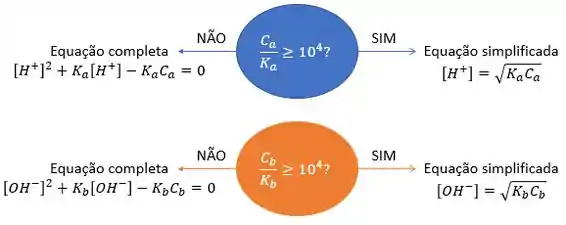
Beleza. Mas volta lá pra fórmula do . Tá vendo aquele ali? O nosso , enquanto o nosso .
Em relação a , o valor de é tão pequeno, que podemos considerar que . Ou seja: .
Fazendo essa aproximação, ficamos com:
E nos livramos da equação de 2° grau! Agora a conta fica simplesmente:
Ou seja, com a nossa aproximação, os cálculos ficaram MUITO mais fáceis e o erro na concentração calculada foi de:
A diferença no pH de 0,01 unidades é difícil até de medir experimentalmente. Então a aproximação foi maneira.
Mas ela é sempre válida?
Não! Ela só é válida quando , ou seja, quando a razão entre esses caras for igual ou maior que .
Para monoácidos fracos e monobases fracas, vale o seguinte esquema:
Ácidos e Bases Fracas
Exercícios Resolvidos
Exercício Resolvido #1
IFRN – Lista de Exercícios de Equilíbrio Qauoso. Professor Albino. Questão 09.
Em um litro de solução aquosa de um ácido forte de foram adicionado de água. Determine o pH da nova solução.
Passo 1
Informação importante: o cara responsável pelo pH ácido do meio é um ácido FORTE!
Ou seja, a ionização é total!
Se fosse um ácido fraco, quanto mais diluído maior a ionização, lembra? Pra ácido forte ela é “sempre” total.
Beleza.. sabendo disso. Vamos ao que interessa.
Como resolver?
Vamos calcular o número de mols de na solução inicial.
Na diluição, só se adiciona água! Então o número de não será alterado.
Com o novo volume, pós diluição, vamos calcular a nova concentração de e, com ela, o novo pH.
Passo 2
Antes da diluição ():
Volume inicial:
Tal que o número de mols de no meio será dado por:
Passo 3
Com a diluição:
Tal que a nova concentração será:
E o pH após a diluição:
Como o pH é na escala de logaritmo, uma diluição de 100 vezes leva a um aumento de duas unidades de pH.
Resposta
pH
Exercício Resolvido #2
UNB – Lista de Química Analítica. Professora Ana Cristi. Questão 08.
Escreva o balanço de massa para a dissociação completa de 0,050 mols de ácido fosfórico () em 1 L de água.
Dados:
Passo 1
No balanço de massa a gente considera que o ácido presente, uma vez adicionado na água, vai coexistir em todas as suas formas possíveis.
Ou seja, quando você coloca em água, ao atingir o equilíbrio você passa a ter uma mistura de , , e em solução. Além, é claro, de , e .
E como , , e são oriundos do ácidos adicionado (concentração analítica do ácido), podemos dizer que a soma desses caras é igual a concentração analítica.
Passo 2
E quem é a concentração analítica?
Portanto:
Resposta
Exercício Resolvido #3
UFRJ – Lista de exercícios de Química Analítica. Prof. Ricardo Santelli. Questão 02.
Calcule o pH de uma solução 0,050 mol/L de . Considere as aproximações e verifique se o erro final será menor que 10%. Dado: .
Passo 1
Vamos começar escrevendo todos os equilíbrios envolvidos, com suas respectivas constantes.
Passo 2
No passo dois verificamos o número de incógnitas e de equações.
Temos 4 incógnitas: .
Temos 2 equações: a do e a do .
Precisamos escrever o balanço de massa (BM) e o balanço de carga (BC).
BM:
Ou seja, todo o adicionado encontra-se na forma de ou .
BC:
Ou seja, a soma das cargas positivas é igual a soma das cargas negativas.
Passo 3
Agora que temos o número de equações igual ao número de incógnitas, podemos fazer as simplificações.
Como estamos adicionando BASE no meio, podemos dizer que:
Portanto, o balanço de cargas pode ser escrito como:
A segunda simplificação nos diz que, como estamos falando de um eletrólito fraco, a concentração da espécie não dissociada será muito maior do que a espécie dissociada.
Portanto, o balanço de massa pode ser escrito como:
Pelas nossas simplificações, vamos considerar, então:
Passo 4
Bora fazer as contas:
Substituindo pelos valores fornecidos:
Tal que:
Show de bola.
Passo 5
Agora temos que verificar as simplificações, né?
Na 1ª simplificação a gente disse que:
E pelo nosso resultado:
Então a primeira aproximação tá valendo! Porque .
Na 2ª simplificação, dissemos que:
Como , a gente considerou que:
Como, sem simplificações:
O erro da simplificação é de:
Portanto, o erro é menor do que os 10% pedidos no enunciado!
Resposta
pH
Erro = 1,87%
Exercício Resolvido #4
UFRJ – Química Analítica. Prof. Ricardo Santelli. Exercício de aula.
Escrever os balanços de massa e de carga para uma solução de ácido sulfúrico em água. Dados: e .
Passo 1
Como o ácido sulfúrico () é diprótico, ele tem dois e duas reações de equilíbrio de ionização:
Além disso, temos o equilíbrio de autoionização da água, que deve ser considerado no nosso balanço de cargas.
Beleza, todo os equilíbrios que estão ocorrendo estão aí em cima.
Hora de fazer os balanços.
Passo 2
No balanço de massa, sabemos que todo o ácido adicionado (ou seja, sua concentração analítica) está no meio como , ou . Portanto:
Como o , podemos considerar que não existe ácido sulfúrico totalmente protonado no meio. Isso é:
Dessa forma, nosso BM será:
Passo 3
Já no balanço de carga, não podemos esquecer de multiplicar o [ por dois. Já que cada mol de tem dois mols de carga!
E o BC fica:
Resposta
BM:
BC:
Exercício Resolvido #5
UNB – Lista de Química Analítica. Professora Ana Cristi. Questão 10.
Escreva a equação do balanço de carga para os seguintes sistemas formados em solução aquosa:
a)
b)
Passo 1
Aqui, o enunciado nos diz os íons presentes em solução aquosa e pede pra que a gente faça os balanços de cargas.
Atenção pra dois pontos principais:
- O equilíbrio é AQUOSO, então não pode esquecer dos íons provenientes da ionização da água!
- Íons com carga maior que a unitária (+2, +3, -2, -3...) são multiplicados pelo módulo da carga na equação de balanço de cargas. Isso porque a gente tá dizendo que o número de CARGAS POSITIVAS em solução é igual ao número de CARGAS NEGATIVAS em solução! O número de cargas negativas no ânion é 2 vezes o número de ânions.
Passo 2
Depois do blábláblá inicial, vamos ao que interessa:
a)
Passo 3
b)
Resposta
a)
b)
Exercício Resolvido #6
UNB – Lista de Química Analítica. Professora Ana Cristi. Questão 11. Modificado.
Deduza, utilizando o método sistemático (equações de balanço de massa, balanço de carga, constantes de dissociação ácida ou básica e constante de auto dissociação da água), equações para o cálculo de pH ou pOH de:
a) ácido forte () com concentração analítica ;
b) base forte () com concentração analítica ;
c) ácido fraco () com concentração analítica ;
d) base fraca () com concentração analítica ;
Use aproximações pertinentes e justifique-as.
Passo 1
a) Se o ácido é forte, não falamos exatamente de um equilíbrio né? Porque ele está tão deslocado para a ionização, que podemos considerar uma reação irreversível.
Então, começamos escrevendo as reações do meio com suas respectivas constantes.
A constante de ionização de ácidos fortes é considerada de valor infinito, uma vez que a concentração do ácido protonado no equilíbrio, aqui o [, tende a zero.
Para o balanço de massa:
E o balanço de carga:
Quanto às aproximações:
Primeiramente, sabendo que o meio é ácido, podemos considerar que .
Dessa forma, o balanço de carga fica:
A segunda aproximação, só é usada para eletrólitos fracos.
Com o que temos já podemos calcular o pH. Olha só:
Passo 2
b) Para uma base forte, consideramos a dissociação total, tal que o é infinito.
Escrevendo as reações do meio com suas respectivas constantes, temos:
Para o balanço de massa:
Pois toda a base encontra-se na sua forma dissociada.
E o balanço de carga:
Quanto às aproximações:
Podemos considerar que , uma vez que quando a gente taca base na água, o meio fica básico, ou seja, com pra caramba.
Dessa forma, o balanço de carga fica:
A segunda aproximação, só é usada para eletrólitos fracos.
E já podemos calcular o pOH. Olha só:
Passo 3
c) Agora estamos tratando de um ácido fraco. Nesse caso, teremos duas reações de equilíbrio no meio: a do ácido e a de autoionização da água.
O nosso balanço de massa, agora deve considerar que o ácido colocado na água está na sua forma protona ou na sua forma ionizada. Portanto, a concentração analítica (inicial) será igual à soma dessas duas formas.
BM:
E o BC:
Ou seja: o somatório das cargas positivas é igual ao somatório de cargas negativas.
E vamos ver as aproximações plausíveis.
Primeiramente, sabendo que o meio é ácido, podemos considerar que .
Dessa forma, o balanço de carga fica:
Na segunda aproximação, consideramos que, como o ácido é fraco, ele vai existir majoritariamente na sua forma protonada. Isto é: , porque poucas moléculas sofrem ionização.
E com isso, nosso BM aproximado fica:
Para ácidos fracos, depois de todas as aproximações cabíveis, usamos a fórmula do para calcular o pH.
Caso , a segunda aproximação não é aconselhada.
Nesse caso, o BM continua como:
Tal que o fica assim:
A concentração de é calculada resolvendo a equação de segundo grau aí de cima. E o pH segue:
Passo 4
d) Hora de fazer tudo isso para uma base fraca. Mais uma vez, teremos duas reações de equilíbrio no meio: a da base e a de autoionização da água.
E o balanço de massa vai considerar que a base colocada na água está parcialmente dissociada. Ou seja, a concentração analítica (inicial) será igual à soma da forma dissociada com a não dissociada.
BM:
E o BC:
Ou seja: o somatório das cargas positivas é igual ao somatório de cargas negativas.
E vamos ver as aproximações que podemos fazer.
Se o meio é básico, podemos considerar que .
Dessa forma, o balanço de carga fica:
Na segunda aproximação, consideramos que, como a base é fraca, a concentração da forma não dissociada será muito maior do que a concentração da forma dissociada.
E com isso, nosso BM aproximado fica:
E pro cálculo do pOH, utilizamos a fórmula do , substituindo as concentrações por valores conhecidos, de acordo com nosso BM, BC e aproximações.
Caso , a segunda aproximação não é aconselhável.
Nesse caso, o BM continua como:
E o fica assim:
A concentração de é calculada resolvendo a equação de segundo grau aí de cima. E o pOH continua sendo calculado assim:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
UNB – Lista de Exercícios de Química Analítica. Professora Ana Cristi. Questão 14.
Calcule o pH para as soluções dos seguintes ácidos fracos. Verifique se as suas aproximações foram válidas:
a) ácido lático () 0,20 mol/L;
b) ácido fórmico ( 0,015 mol/L.
Passo 1
Essa coisa de verificar se suas aproximações são válidas é bem relativa. Os professores aplicam critérios diferentes.
Um deles é aquele que a gente mostrou do . Outros pedem pra calcular o erro associado à aproximação e dizem o que eles consideram aceitável.
Aqui, vamos mostrar esses dois modos.
Passo 2
a) Começamos com as reações de equilíbrio.
Em seguida, fazemos os balanços:
Vamos considerar que, estando em meio ácido, . E o BC fica simplesmente:
A segunda aproximação diz que, para ácidos fracos, a forma não ionizada existe em muito maior quantidade no meio.
Tal que o balanço de massa é considerado como sendo:
Jogando tudo na fórmula do :
E agora a gente checa as nossas simplificações.
Será que ?
Bem, se , então e a primeira aproximação está ok!
E será que foi uma boa aproximação?
Considerando que , o erro fica:
E a aproximação é boa?
A resposta certa é: DEPENDE!
Se o seu professor exige um erro menor que 1%, ela é bem ruinzinha. Se o seu professor exige um erro menor que 5%, tá de bouas.
Caso você ache ela ruinzinha ou se utilizou o critério do , o cálculo do pH deve ser feito sem a segunda aproximação. Ou seja:
E a gente vai ter que resolver aquela equação de segundo grau:
DEU O MESMO PH!!! Parece que a aproximação era válida sim!!!
Passo 3
b) Começamos com as reações de equilíbrio.
Em seguida, fazemos os balanços:
Como o meio estará ácido, a primeira simplificação será considerar que . E o BC fica simplesmente:
A segunda aproximação diz que, para ácidos fracos, a forma não ionizada existe em muito maior quantidade no meio.
Tal que o balanço de massa é considerado como sendo:
Jogando tudo na fórmula do :
E agora a gente checa as nossas simplificações.
Será que ?
Bem, se , então e a primeira aproximação está ok!
E será que foi uma boa aproximação?
Considerando que , o erro fica:
E a aproximação é boa?
A resposta certa ainda é depende. Mas vamos combinar que um erro superior que 10% já é bem ruinzinho né;
Além disso, o critério do , também nos indica que o cálculo do pH é uma missão para a equação de segunda ordem.
No item b a aproximação foi pior porque:
- O do ácido era maior, então, na verdade, a gente vai ter um pouco mais de ácido ionizado.
- A concentração era menor, e quanto menor a concentração, mais extensa é a ionização.
Resposta
a) pH
b) pH
Exercício Resolvido #8
UNB – Lista de Exercícios de Química Analítica. Professora Ana Cristi. Questão 15.
Calcule o pH para as soluções das seguintes bases fracas. Verifique se as suas aproximações foram válidas:
a) metilamina () 0,020 mol/L;
b) amônia ( 0,10 mol/L.
Passo 1
a) Começamos com as reações de equilíbrio.
Em seguida, fazemos os balanços:
Como o meio é básico, nossa primeira aproximação será que . E o BC fica simplesmente:
A segunda aproximação diz que, para bases fracas, a forma não dissociada existe em muito maior quantidade no meio.
Tal que o balanço de massa é aproximado para:
Jogando tudo na fórmula do :
Mas será que as nossas simplificações foram boas?
Primeiro consideramos que.
Se , então e a primeira aproximação está ok!
E será que foi uma boa aproximação?
Considerando que , o erro fica:
E a aproximação é bem ruinzinha né.
Pelo critério de :
Não tem jeito, precisamos resolver a equação de segundo grau:
Passo 2
b) Começamos com as reações de equilíbrio.
Em seguida, fazemos os balanços:
Como o meio é básico, nossa primeira aproximação será dizer que . E o BC fica simplesmente:
A segunda aproximação diz que, para bases fracas, a forma não dissociada existe em muito maior quantidade no equilíbrio.
Tal que o balanço de massa é aproximado para:
Jogando tudo na fórmula do :
Mas será que as nossas aproximações foram boas?
Primeiro consideramos que.
Se , então e a primeira aproximação está ok!
E será que foi uma boa aproximação?
Considerando que , o erro fica:
Considerando uma tolerância de, por exemplo, 5%, a aproximação seria considerada ok e o cálculo de pH terminaria aqui.
Pelo critério de :
Por esse critério, no entanto, a gente precisa resolver a equação de segundo grau.
Resposta
a) pH
b) pH
Exercício Resolvido #9
UFRJ – Química Analítica. Prof. Ricardo Santelli. Exercício de aula.
Calcule o pH de um solução de .
Passo 1
A sacada dessa questão é você perceber que, nesse caso, o está tão diluído, mas tão diluído, que a autoinozação da água passa a ser relevante.
Por isso, vamos ter que considera-la nos cálculos.
A concentração de na água pura é de mol/L e a gente tá adicionando mol/L pela adição do .
Passo 2
Reações:
Passo 3
Balanços:
Afinal de contas, não sobra nenhum não ionizado, porque o cara é um ácido forte.
Passo 4
Como o ácido está MUITO diluído, não podemos fazer nossas simplificações. O jeito vai ser manipular os balanços até conseguir substituir todo mundo na equação do por coisas que a gente possa calcular.
Sabemos o valor de e queremos descobrir o . Precisamos colocar em função de ou .
Pelo BC:
Pelo BM:
Beleza, já podemos calcular!
E bora resolver a equação de segundo grau:
Resposta
pH