Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 1.Problemas Numéricos - Ex. 3
1.3 A lei de Charles também se escreve como , onde é a temperatura Celsius, é uma constante, e é o volume da amostra do gás a 0°C. Para o nitrogênio a 0°C, obtiveram-se os seguintes valores de :
Com esses dados, estime o melhor valor do zero absoluto de temperatura na escala Celsius.
Passo 1
Opaaa... nessa questão vamos usar a equação do gás perfeito:
E lembrar que a temperatura absoluta é a Kelvin... então queremos achar quanto é 0 K em graus Celsius.
Passo 2
Bom... o intuido aqui não é usar o -273 bla blá blá que a gente conhece, mas sim chegar nele.
Então vamos lá...
Usando a equação do gás perfeito:
Substituindo:
E fazendo a regressão linear:
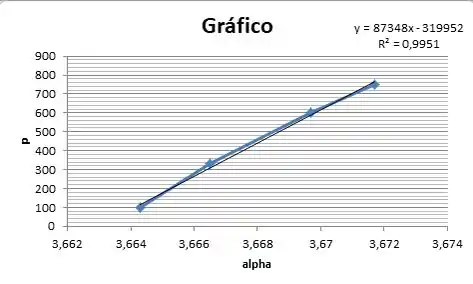
Comparando as equações:
Então:
Mas repara que os dados de têm um , então:
Resposta
Exercícios de Livros Relacionados
A massa específica de um composto gasoso é 1,23k g m - 3 , a 330 K e 20 k P a . Qual a massa molar do composto?
A massa específica do ar a - 85 ℃ ℃ é 1,877g d m - 3 , a 0 ℃ ℃ é 1,294g d m - 3 e a 100 ℃ ℃ é 0,946g d m - 3 . A partir desses dados, e admitindo que o ar obedece a lei de Charles, determine um valor
Uma mistura de gás consiste em 320 mg de metano, 175 mg de argônio e 225 mg de neônio. A pressão parcial do neônio a 300 K é de 8,87 kPa. Calcule (i) o volume e (ii) a pressão total da mistura.
Os seguintes dados foram obtidos para o oxigênio a 273,15 K. A partir deles calcule o melhor valor da constante dos gases R e também o melhor valor da massa molar do O 2 .
(a) Dado que a densidade de massa do ar a 0,987b a r e 27 ℃ ℃ é 1,146k g m - 3 . Calcule a fração molar e a pressão parcial de nitrogênio e oxigênio assumindo que (i) o ar consiste apenas desses dois