17 – A molécula de fanantreno pertence ao grupo C2v, com o eixo C2 no plano da molécula.
A) Dê as representações irredutíveis cobertas pelos orbitais C2px e obtenha as combinações lineares adaptadas à simetria.
B) Use os resultados da parte (A) para calcular o determinante secular de Hückel.
C) Que estados do fenantreno podem ser atingidos por transições de dipolo elétrico a partir do respectivo estado fundamental (que é totalmente simétrico)?
Passo 1
Vamos começar esboçando a molécula de fenantreno mostrando os átomos de carbono designados tal como mostrado abaixo:
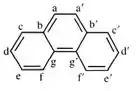
Passo 2
A)
Para obtermos as representações irredutíveis, vamos considerar como base os orbitais 2p no sistema π de elétrons.
Para encontrarmos as representações irredutíveis, tem-se que cada base é transformada sob as operações de simetria do grupo C2v. Para achar o caractere de uma operação nesta base, temos que somar os coeficientes dos termos desta base que são inalterados pela operação.
A seguinte tabela de caracteres pode ser usada:

Onde, X representa a soma dos coeficientes.
Passo 3
Assim, para acharmos as representações irredutíveis que são abrangidas pelos orbitais 2p, vamos multiplicar os caracteres na representação dos orbitais pelos caracteres das representações irredutíveis, somar estes produtos, e dividir a soma pela ordem h do grupo. A tabela a seguir ilustra este procedimento:

A representação dos orbitais pode ser expressa como:
Passo 4
Para encontrarmos as combinações lineares adaptadas à simetria, vamos usar a tabela acima, fazendo a multiplicação de cada caractere das espécies das representações irredutíveis, somando os termos na coluna e dividindo pela ordem do grupo.
Tendo o procedimento como foi descrito, as combinações lineares serão:
-Para A1: Como a soma resultante foi nula, então não há combinação linear adaptada à simetria neste grupo;
-Para A2: Haverá sete combinações lineares distintas, que são:
-Para B1: Para este, assim como para A2, terá sete combinações distintas:
-Para B2: Analogamente para A1, este também não terá nenhuma combinação linear, pois a soma resultante é zero;
Passo 5
B)
Seguindo a rotulação feita para cada átomo de carbono do fenantreno, assim, o determinante secular de Hückel pode ser montado como:

Passo 6
C)
O estado fundamental da molécula tem simetria A1 pelo fato de que sua função de onda é o produto de uma dupla de orbitais ocupado, e o produto de quaisquer dois orbitais de mesma simetria tem caractere A1. Se uma transição dever ser permitida, a transição do dipolo deve ser não nula, na qual por sua vez só pode ocorrer se a representação do produto ψf*μψi incluir a simetria total da espécie A1.
Considerando as primeiras transições da outra função de onda A1, na qual neste caso vamos ter o produto A1μA1. Sendo assim, agora temos que A1A1 = A1, e o único caractere que retorna A1 quando A1 multiplica por A1 é o próprio A1.
A componente z do operador dipolo se torna a espécie A1, então as transições de z-polarizado A1
A outra possibilidade é a transição de um orbital de uma simetria para outra, por exemplo pegando A1 e B1, e neste caso, a função de onda do estado excitado terá simetria de A1B1 = B2 de dois orbitais únicos no estado excitado. A simetria da transição do dipolo, então, é A1μA2=μB2, e a única espécie que produz A1 quando multiplicado por B2 é B2. Agora tem-se que o componente y do operador dipolo se torna a espécie B2, então estas transições também são permitidas, com y polarizado.
Resposta
A)
-Para A1: Nenhuma combinação.
-Para A2:
-Para B1:
-Para B2: Nenhuma combinação.
B)
