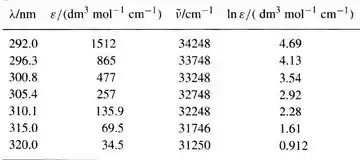
25 – O ozônio absorve radiação ultravioleta numa parte do espectro eletromagnético que tem energia suficiente para romper o DNA dos organismos vivos e que não é absorvida por outros componentes atmosféricos. Essa faixa espectral, identificada como UV-B, cobre, aproximadamente, os comprimentos de onda de 290 nm até 320 nm. O coeficiente de extinção molar do ozônio, nesse intervalo, aparece na tabela seguinte.

Calcule o coeficiente de absorção integrado do ozônio sobre o intervalo de comprimento de onda 290-320 nm.

Sugestão: ε(v) pode ser bem ajustado por uma função exponencial.

Como foi dito no enunciado, que ε(v) pode ser bem ajustado por uma função exponencial, assim podemos determinar uma relação de ε(v) com v como uma reta do tipo y = ax + b, pegando o termo dependente y como sendo o Ln de ε, e o termo independente x sendo v, fincando da seguinte forma:

Explicitando o termo de ε, aplicando exponencial em ambos os lados da Eq2:

Assim, vamos precisar determinar os coeficientes da reta, a e b, pela eq. da reta Eq2 fazendo um ajuste dos dados a uma reta, usando os dados fornecidos.

Vamos montar uma nova tabela, agora com os valores de v e ln(ε), para depois plotarmos o gráfico e pegarmos a eq. da reta por regressão linear.

Sendo

Assim, a tabela será:

Com os dados da tabela, podemos plotar o gráfico de ln(ε) versus v, e obtermos q eq. da reta de ln(ε) vs v:

O gráfico é:

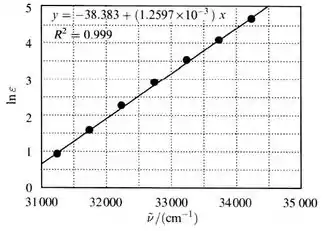
Veja que a eq. da reta é:

Assim, como

Logo,

Portando

Com os coeficientes determinados, a função de ε(v) será, pela Eq3:

Onde,

Assim,

Calculando o coeficiente de absorção integrado pela Eq1:

Substituindo:

Integrando sobre o intervalo de comprimento de onda 290-320 nm.

Onde,

Assim,