Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 7.1 - Ex. 42
7.42 Use as seguintes informações para constuir uma curva de aqucimento para o bromo, d -7,2°C até 70,0°C. A capacidade calorífica molar do bromo líquido é e a do bromo como vapor é . A entalpia de vaporização do bromo líquido é . O bromo funde em -7,2°C e entra m ebulição em 58,78°C.
Passo 1
Lembrando que a equação de calor que corresponde à mudança de fase é do tipo
Podemos observar que a equação é independente da temperatura, então concluímos que a entalpia de vaporização corresponde a uma parte paralela ao eixo do Calor fornecido.
Agora vamos lembrar da equação que tem capacidade calorífica (equação (6b)
Para termos uma melhor vizualização vamos mexer um pouco na equação, pois, nos gráficos temos no eixo y e Calor fornecido no eixo x
Vemos que é uma equação de reta com coeficiente angular .
Agora vamos puxar só um pouquinho os conhecimentos e lembrar que quanto maior o coeficiente angular da reta, maior a sua inclinação. Como gás é maior que do líquido, então do líquido é maior que gás. Sendo assim, o coeficiente angular no líquido é maior e, consequentemente, a reta é mais inclinada.
Passo 2
Construindo um esboço do gráfico esperado, temos
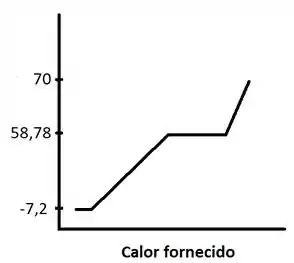
Como não foi especificada nenhuma informação sobre a entalpia de fusão, vamos representar com uma pequena paralela ao eixo do calor fornecido em -7,2°C somente para representar que nessa temperatura ocorre a mudança de fase, como ele diz, o bromo congela. Depois outra reta paralela vai aparecer em 58,78°C para representar a vaporização do bromo.
Por conclusões que tiramos anteriormente, entre -7,2°C e 58,78, representamos o aquecimento do líquido, com uma reta menos inclinada do que a reta que vem depois do 58,78°C.
Resposta
Ei, a resposta está no passo a passo :)