Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 11
Uma análise volumétrica de cálcio realizada em triplicata de uma amostra de soro sangüíneo, de um paciente que se acreditava estar sofrendo de hipertireoidismo, produziu os seguintes dados: meq de Ca/L 3,15; 3,25 e 3,26. Qual o limite de confiança, a 95%, para a média dos dados, considerando:
(a) A ausência de informação prévia sobre a
precisão da análise?
(b) s S s 0,056 meq de Ca/L?
Passo 1
Fala aí! Para resolvermos essa aqui, temos que lembrar da expressão usada para encontrar o intervalo de confiança para a média de N medidas, quando não se tem certeza a respeito da precisão :
Ali, s vai ser nossa melhor estimativa da precisão e t vai nos ajudar a encontrar o nível de confiança a partir da seguinte tabela:
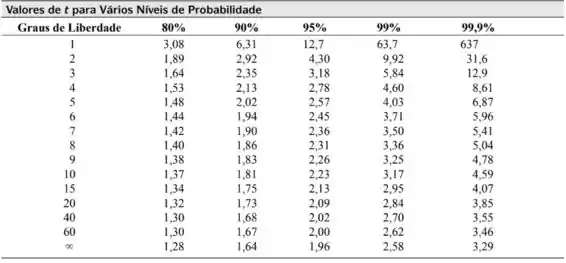
Para começar, vamos calcular a média e o desvio padrão dos dados fornecidos:
Com isso, podemos aplicar naquela expressão lá do começo, considerando para dois graus de liberdade em um limite de confiança de 95%, como mostrado na tabela.
Agora, considerando o desvio igual a 0,056:
Resposta
(a) .
(b) .