Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 6
O último resultado de cada conjunto de dados do Problema 7-4 pode ser um valor anômalo. Aplique o teste Q (nível de confiança de 95%) para determinar se há ou não base estatística para a rejeição.
Passo 1
Fala aí! Esse teste Q é uma saída muito esperta, porém simples, para se decidir se um resultado anômalo deve ser mantido ou descartado. A ideia é o seguinte: pegamos o resultado absoluto da diferença entre o valor em questão e seu vizinho mais próximo e o dividimos pela faixa do conjunto inteiro. A equação fica assim:
Queremos aplicar essa expressão em cada um dos conjuntos mostrados.
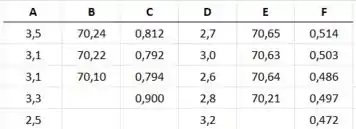
Portanto, para o conjunto A, teremos o seguinte:
Agora, comparamos o valor obtido com a seguinte tabela:
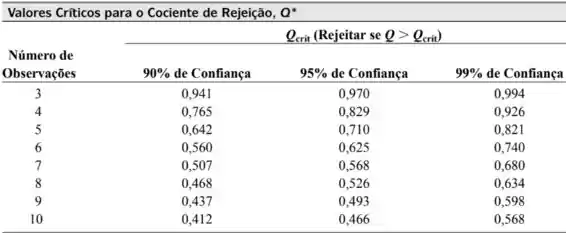
Repare que, para cinco medidas, o Q crítico é 0,71 a um nível de confiança de 95%. Como 0,8 é maior que 0,71, devemos descartar o valor anômalo em um nível de confiança de 95%.
Passo 2
Agora é só repetir o processo e fazer a análise para os demais conjuntos.
Dessa vez, temos somente três medidas, então o Q crítico passa a ser 0,97 a um nível de confiança de 95%. Por isso, devemos manter o valor de 0,86 do conjunto B.
Passo 3
Para quatro medidas, o Q crítico a 95% de confiança é igual a 0,829. Tal como no Passo 1, o valor obtido é maior que isso, então devemos descartar o resultado anômalo.
Passo 4
Esse aqui passou perto, mas devemos mantê-lo, pois o Q crítico para cinco medidas é 0,71.
Passo 5
Esse aqui passou longe. Vamos descartá-lo, pois o Q crítico para quatro medidas a 95% de confiança é só 0,829.
Passo 6
Pra finalizar:
Esse valor vai ser mantido, pois é menor que o Q crítico para cinco medidas.
Resposta
Os últimos resultados dos conjuntos B, D e F devem ser mantidos, os demais serão descartados a um nível de confiança de 95%.