Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 9

Quantas réplicas de medidas são necessárias para diminuir os intervalos de confiança de 95% e 99% para a análise descrita no Problema 7-7 para 1,5 mg de Fe/mL?

Passo 1

Fala aí! Para resolvermos essa aqui, temos que lembrar da expressão usada para encontrar o intervalo de confiança para a média verdadeira:

I C = x - ± z σ N

Ali, z vai nos ajudar a encontrar o nível de confiança a partir da seguinte tabela:

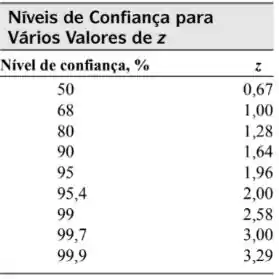
Com isso, vamos fazer um processo inverso do que estamos acostumados. Se liga, o que queremos descobrir aqui é o número de medidas (o N no denominador) para que os intervalos de confiança de 95% e 99% sejam ± 1,5   μ g / m L .

9 5 %   I C = 1 , 96 ⋅ 2,4 N = 1,5

Vamos trocar o 1,5 e o N de lugar.

N = 1 , 96 ⋅ 2,4 1,5 = 3,136

Então:

N 2 = 3,136 2 → N = 9,8 ≈ 10   m e d i d a s

Passo 2

Vamos repetir o processo para 99% de confiança:

9 9 %   I C = 2,58 ⋅ 2,4 N = 1,5

N = 4,128

N = 17   m e d i d a s

Resposta

Para diminuir os intervalos de confiança de 95% e 99% para 1,5 mg de Fe/mL são necessárias 10 medidas e 17 medidas, respectivamente.

Exercícios de Livros Relacionados

Descreva com suas próprias palavras por que o intervalo de confiança em relação à média de cinco medidas é menor que aquele para um único resultado.
Discuta como a dimensão do intervalo de confiança da média é influenciada pelos seguintes aspectos (todos os outros fatores são constantes):(a) O tamanho N da amostra.(b) O nível de confiança.(c) O de
Considerando um grande número de medidas de forma que s seja uma boa estimativa de e, determine que nível de confiança foi usado para cada um dos intervalos de confiança.
Lord Rayleigh preparou amostras de nitrogênio por diversos métodos diferentes. A densidade de cada amostra foi medida como a massa de gás necessária para encher um determinado frasco, sob uma certa te
Dois métodos analíticos diferentes foram usados para determinar cloro residual em efluentes de esgoto. Ambos os métodos foram usados nas mesmas amostras, mas cada amostra foi coletada de vários locais