Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 5

Calcule o intervalo de confiança de 95% para cada conjunto de dados do Problema 7-4 se s for uma boa estimativa de s e tem um valor de: *conjunto A, 0,20; conjunto B, 0,070; *conjunto C, 0,0090; conjunto D, 0,30; *conjunto E, 0,15; conjunto F, 0,015.

Passo 1

Fala aí! Para resolvermos essa aqui, temos que lembrar da expressão usada para encontrar o intervalo de confiança para a média verdadeira:

I C = x - ± z σ N

Além disso, vamos precisar da seguinte tabelinha:

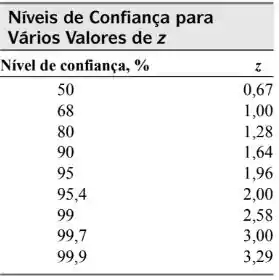
Ainda, a tabela que montamos no exercício anterior também vai nos ser bastante útil:

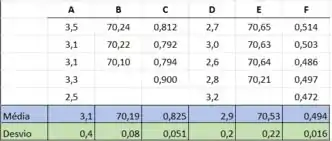
Com isso, podemos começar a resolver o problema. Se liga, para o conjunto A, tínhamos uma média de um total de 5 medidas igual a 3,1; com o z correspondente ao nível de confiança de 95%, ficamos com:

I C = 3,1 ± 1,96 ⋅ 0,20 5 = 3,1 ± 0,18

Passo 2

Repetindo este processo para os demais conjuntos, vamos obter os seguintes resultados:

I C B = 70,19 ± 1,96 ⋅ 0,070 5 = 70,19 ± 0,061

I C C = 0,825 ± 1,96 ⋅ 0,0090 4 = 0,825 ± 0,0088

I C D = 2,9 ± 1,96 ⋅ 0,30 5 = 2,9 ± 0,26

I C E = 70,53 ± 1,96 ⋅ 0,15 4 = 70,53 ± 0,147

I C F = 0,494 ± 1,96 ⋅ 0,015 5 = 0,494 ± 0,013

Resposta

I C A = 0,18

I C B = 0,061

I C C = 0,00 9

I C D = 0,26

I C E = 0,1 5

I C F = 0,013

Exercícios de Livros Relacionados

Um químico obteve os seguintes dados para o porcentual de lindano em análises em triplicata de uma preparação comercial de um inseticida: 7,47; 6,98 e 7,27. Calcule o intervalo de confiança, a 90%, da
Um método baseado em absorção atômica, desenvolvido para a determinação de cobre em combustíveis, gerou um desvio padrão combinado scomb 0,32 mg de Cu/Ml (s S s). A análise do óleo do motor de uma aer
Um método baseado em absorção atômica, desenvolvido para a determinação de ferro presente em óleo usado de motores a jato, apresentou um desvio padrão s 2,4 mg de Fe/mL, a partir de 30 análises realiz
Um método padrão usado na determinação de glicose em soro sangüíneo apresenta um desvio padrão de 0,40 mg/dL. Se s 0,40 mg/dL for uma boa estimativa de s, quantas réplicas de determinações deveriam se
Considere os seguintes conjuntos de réplicas de medidas:Calcule a média e o desvio padrão para cada um dos seis conjuntos de dados. Calcule o intervalo de confiança de 95% para cada conjunto de dados.