Para cada um dos orbitais listados no exercício 53, dê os valores possíveis do número quântico magnético.

Orbitais:(a) 6p; (b) 3d; (c) 2p; (d) 5f.

O número quântico magnético para um elétron em um subnível vai depender apenas do tipo de orbital que conforma esse subnível. A seguinte tabela dá os valores possívels dos números quânticos magnéticos, :

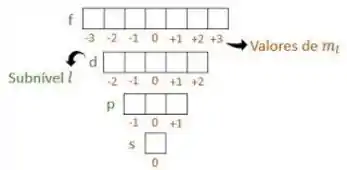
O elétron pode ocupar qualquer uma dessas “casinhas”, que representam os orbitais, no subnível, contanto que a “casinha” esteja desocupada. Conforme elas vão sendo preenchidas, até acabar casinhas totalmente vazias, os próximos elétrons começam a ocupar o espaço faltante, já que em cada orbital cabem sempre, no máximo, 2 elétrons.

Como só queremos saber as possibilidades dos números quânticos magnéticos, , basta a gente identificar o tipo de orbital do subnível (e isso é a coisa mais fácil do mundo, já que o próprio subnível indica o orbital!) e olhar na tabela pra ver quantas são as possibilidades, e escrevê-las! Para os orbitais listados no enunciado, vamos ter:

(a) -1, 0 e +1.

(b) -2, -1, 0, +1 e +2

(c) -1, 0 e +1

(d) -3, -2, -1, 0, +1, +2 e +3