Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 18.Questões e Problemas - Ex. 17
Calcule o potencial de um eletrodo de platina imerso em uma solução que seja:
Passo 1
Nesta tarefa, precisamos calcular o potencial de um eletrodo de platina.
A tendência de um metal oxidar é uma medida do potencial do eletrodo. Diferentes metais têm diferentes tendências de oxidação e, portanto, diferentes potenciais de eletrodo.
Em geral, um metal imerso em uma solução de seus próprios íons forma um semi-membro correspondente.
Em uma célula galvânica, a energia química é convertida espontaneamente em energia elétrica. A célula galvânica consiste em duas meias-células diferentes conectadas por um condutor e uma ponte eletrolítica. O eletrodo no qual ocorre o processo de oxidação é chamado de ânodo e é o pólo negativo da célula. O eletrodo no qual ocorre o processo redução é chamado de cátodo e é o pólo positivo da célula.
O potencial do eletrodo pode ser calculado usando a equação de Nernst.
Se tivermos uma reação:
a equação de Nernst é:
Se substituirmos valores numéricos por constantes e convertermos para logaritmo de base 10 obtemos:
onde E° é o potencial de eletrodo padrão e nn é o número de mols de elétrons para semirreação
Passo 2
- Temos eletrodo de platina imerso em e
- A reação no eletrodo de platina é:
- Nós temos eletrodo de platina imerso em solução tamponada em pH 5.55 e saturado com a 1 atm.
- Temos eletrodo de platina imerso em 0,1996 M , 0,0789 M e 0,08 M
- Temos eletrodo de platina imerso em solução preparada misturando 50 mL de 0.0607 M e 50 mL de 0.1 M .
- Temos eletrodo de platina imerso em solução preparada misturando 25 mL de 0,0832 M e 50 mL de 0,00628 M de para pH 1.
A reação no eletrodo de platina é:
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é:
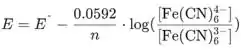
A dissociação de
De acordo com a reação, os mols de são iguais aos mols de , então:
A dissociação de:
De acordo com a reação, os mols de são iguais aos mols de , então:
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
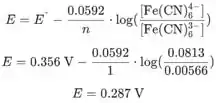
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é:
A dissociação de
De acordo com a reação, para cada mol de a 2 mols de , então a concentração de é:
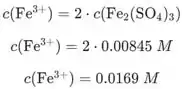
A dissociação de
De acordo com a reação, os mols de são iguais aos de , então a concentração de é igual a de
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo
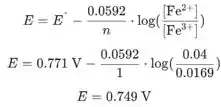
Passo 3
A reação no eletrodo de platina é:
O potencial de redução padrão para esta reação é zero.
A equação de Nernst para esta reação é:
Calculamos a concentração de usando o pH da solução:
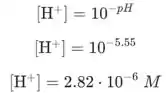
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
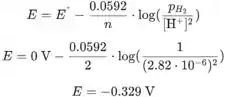
A reação no eletrodo de platina é
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é:
A concentração de é igual a concentração de
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
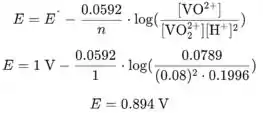
Passo 4
A reação no eletrodo de platina é:
O potencial de redução padrão para esta reação é:
A equação de Nernst para esta reação é:
Precisamos calcular a quantidade restante de e formou . Primeiro calculamos a quantidade de que é consumido. Usamos concentração de e volume:
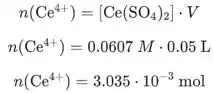
Então, calculamos a quantidade de que é consumido usando a concentração de e volume:
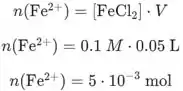
A quantidade de que é formado é igual à quantidade de que é consumido:
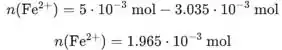
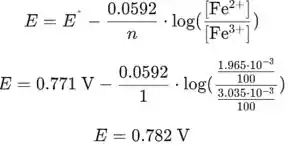
A reação no eletrodo de platina é:
O potencial de redução padrão para esta reação é:
A reação entre e
A quantidade de consumida é:
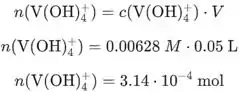
A quantidade de consumida é
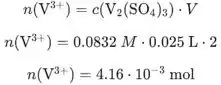
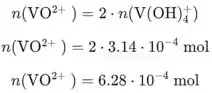
A quantidade remanescente de
Calculamos a concentração de usando o pH da solução:
Agora colocamos valores na equação de Nernst para obter o potencial do eletrodo:
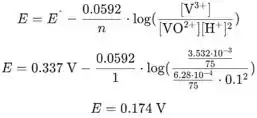
Resposta
a) E = 0.287 V b) E = 0.749 V c) E = 0.329 V d) E = 0.894 V e) E = 0.782 V f) E = 0.174 V