Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 13.Exercícios - Ex. 20a

Os cinco primeiros níveis de energia vibracional do H C l estão a 1481,86 ; 4367,50 ; 7149,04 ; 9826,48   e   12399,8   c m - 1 . Calcule a energia de dissociação da molécula em inverso de centímetros e em elétrons-volt.

Passo 1

E aí, bora começar a resolver mais uma questão juntos?

Se liga então!

Começamos o nosso problema definindo algumas equações:

∆ G v + 1 / 2 = v - - 2 v + 1 x e v -

Onde

∆ G v + 1 / 2 = G v + 1 - G v

Portanto, desde:

∆ G v + 1 / 2 = 1 - 2 x e v - - 2 v x e v -

Plotando um gráfico de ∆ G v + 1 / 2 contra v , ele deve fornecer uma linha reta que fornece - 2 x e v - da interceptação em ( 1 - 2 x e ) v - em v = 0 .

Elaboramos a seguinte tabela:

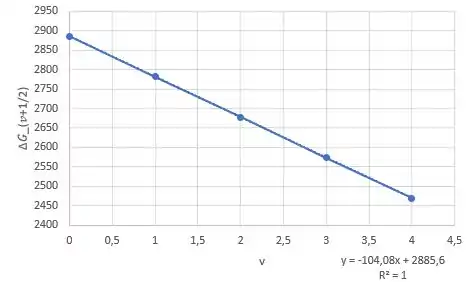
Passo 2

Temos que a interceptação se encontra em 2885 , 6   c m - 1 e a inclinação é  - 2 x e v = - 104,11   c m - 1 , consequentemente:

x e v - = 104,11 2 = 52,06   c m - 1

Uma vez  v - - 2 x e v - = 2885 , 6   c m - 1 que segue v - = 2989,91   c m - 1 .

A energia de dissociação pode ser obtida assumindo que a molécula é descrita por um potencial de Morse e que a constante  D e na expressão para o potencial é uma primeira aproximação adequada para ele. Então:

D e = v - 4 x e = v - 2 4 x e v - = 2989,91 2 4 ⋅ 52,06 = 42,93 × 10 3   c m - 1

Convertendo:

D e = 42,93 × 10 3   c m - 1 × 1   e V 8065,5   c m - 1

D e = 5,32   e V

Porém, a profundidade do poço de potencial ( D e ) difere da energia de dissociação da ligação ( D 0 ), pela energia do ponto zero, assim:

D 0 = D e - v - 2

Substituindo os dados:

D 0 = 42,93 × 10 3 - 2989,91 2

D 0 = 4,14 × 10 4   c m - 1

Convertendo:

D 0 = 4,14 × 10 4   c m - 1 ⋅ 1   e V 8065,5   c m - 1

D 0 = 5 , 1373   e V

E acabamos!

Até a próxima questão!

Resposta

D e = 42,93 × 10 3   c m - 1

D e = 5,32   e V

D 0 = 4,14 × 10 4   c m - 1

D 0 = 5 , 1373   e V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O número de onda da transição de vibração fundamental do C l 35 2 é 564,9c m - 1 . Calcule a constante de força da ligação m C l 35 = 34,9688u .
Calcule a diferença percentual entre os números de onda das vibrações fundamentais do N a 23 C l 35 e N a 23 C l 37 na hipótese de as respectivas constantes de força serem iguais.
Calcule os números relativos de moléculas de C l 2v - = 559,7c m - 1 no estado fundamental e no primeiro estado excitado de vibração a (a) 298K , e (b) 500K .
Para a molécula de O 16 2 , os valores de ∆ G das transições v = 1 ← 0 ,2 ← 0 , e 3 ← 0 são, respectivamente, 1556,22 3088,28 e 4596,21c m - 1 . Calcule v - e x e . Admita que y e seja nulo.
Os cinco primeiros níveis de energia vibracional do H I estão a 1 144,83 ; 3374,90 ; 5525,51 ; 7596,66e9588,35c m - 1 . Calcule a energia de dissociação da molécula em inverso de centímetros e em elét