Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 16.1 - Ex. 67
Os ligantes que podem interagir com um centro de metal formando uma ligação do tipo são comumente chamados de ácidos e bases . A definição de ácidos e bases são semelhantes às usadas para a acidez de Lewis. Um ácido é um ligante que pode aceitar elétrons usando orbitais do tipo , e uma base doa elétrons usando orbitais do tipo . Com base nessas definições, classifique os seguintes ligantes como ácidos ou bases ou nenhum dos dois:
- ;
- ;
- ;
- en.
Coloque-os em ordem crescente de divisão do campo de ligantes.
Passo 1
Legal galera, vamos para mais uma!
Começando pela letra a, vamos fazer o diagrama para o íon
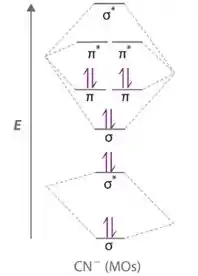
O íon CN é um ligante ácido capaz de aceitar elétrons no orbital * vazio criado pela ligação múltipla .
Passo 2
Para o íon , de distribuição:
Sendo assim, todos os seus orbitais estão preenchidos, logo ele pode atuar como uma base , doando os elétrons do seu orbital p para um orbital vazio d do metal.
Tranquilo até aqui?
A distribuição eletrônica, no caso da água é dado por:
A também possui um par de elétrons "extra" que podem ser doados a um centro de metal, tornando-o uma base fraca, capaz de doar os elétrons do seu orbital p para um orbital vazio d do metal.
Passo 3
Já o ligante em não é nem um ácido nem uma base , porque não possui orbitais antiligantes do tipo vazios e não possui pares solitários extras de elétrons para doar.
De acordo com a série espectroquímica podemos analisar a ordem crescente dos ligantes:
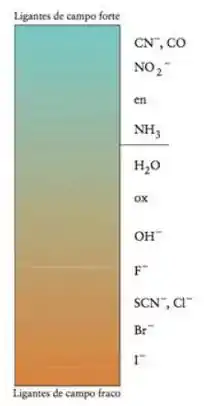
Então:
Ou seja:
Shoow né?!
Resposta
- ;
- ;