Desenhe um diagrama de níveis de energia de orbitais (como os das Figs. 16.27 e 16.29) mostrando a configuração dos elétrons d sobre o íon de metal nos seguintes complexos:
- ;
- ;
- ;
- ;
Preveja o número de elétrons não emparelhados para cada complexo.
Passo 1
Bora galera, começar mais uma!
Aqui nós temos seis ligantes monodentados, ou seja, o numero de coordenação do metal é seis.
Com isso podemos saber a estrutura formada, certo? Advinham qual?
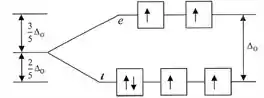
Acertou quem disse octaédrica, ok?! Então já sabemos qual diagrama devemos usar, Fig 16.27.
Para completar precisamos saber dos elétrons de valência do ferro II:
[Fe2+] = [Ar] 3d6
Então temos seis elétrons na camada de valência.
Então temos seis elétrons na camada de valência. Como o ligante possui o campo fraco, os campos de energia estão mais próximos, logo devemos esperar que os elétrons ocupem todos os orbitais vazios, resultando em um número máximo de elétrons desemparelhados:
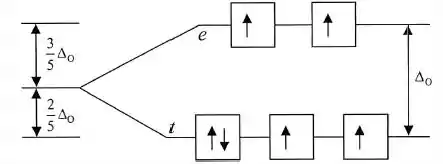
Quatro elétrons desemparelhados, ou seja, molécula paramagnética.
Próximaa!
Passo 2
Aqui nós temos quatro ligantes monodentados, ou seja, o numero de coordenação do metal é quatro.
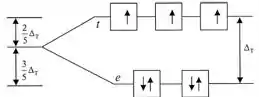
Ou seja, estrutura tetraédrica ! Então usaremos o diagrama da Fig 16.29.
Para completar precisamos saber dos elétrons de valência do cobalto:
[Co2+] =[Ar] 3d7
Então temos sete elétrons na camada de valência.
Aqui também temos ligante de campo fraco, então a distribuição será:
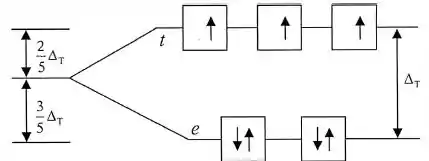
Temos três elétrons desemparelhados, molécula paramagnética.
Passo 3
Na letra c também temos o cobalto, mas cobalto III e não o dois como vimos na letra b, ok?
[Co3+] =[Ar] 3d6
Então temos seis elétrons na camada de valência.
Como temos seis ligantes, o número de coordenação é seis, ou seja, octaédrica!
A grande questão aqui é que o ligante é de campo forte.
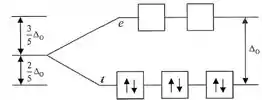
Nestes casos, os níveis de energia estão muito separados e devemos esperar que os elétrons se emparelhem nos orbitais de energia mais baixa, resultando em menos elétrons desemparelhados:
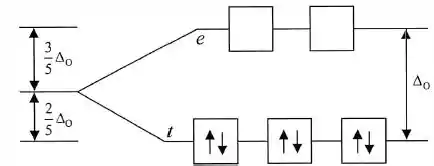
Nenhum elétron desemparelhado, molécula diamagnética!
Passo 4
Na letra d temos a mesma configuração eletrônica da anterior, com ligante de campo fraco.
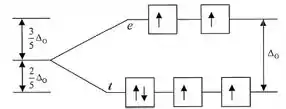
Então temos seis elétrons de valência espalhados por todos os orbitais, como a geometria é octaédrica:
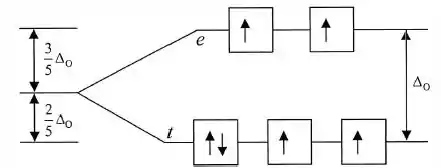
Por isso, quatro elétrons desemparelhados.
Mais uma prontinha galeraaa!
Resposta
- Elétrons desemparelhados: 4
- Elétrons desemparelhados: 3
- Elétrons desemparelhados: 0
- Elétrons desemparelhados: 4