Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 14.1 - Ex. 24

Determine a constante de velocidade para cada uma das seguintes reações de primeira ordem:

  1. 2 A → B +   C , sabendo que a concentração de A decresce a um quarto do seu valor inicial em 61 min;
  2. 2 A → B +   C , sabendo que [ A ] 0 =   0,021   m o l · L - 1 e que após 45 s a concentração de B aumenta para   0,0 0 1 25   m o l · L - 1 ;
  3. 2 A → 3 B +   C , dado que [ A ] 0 =   0,0 6   m o l · L - 1 e que após 10,8 min a concentração de B cresce para 0,040   m o l · L - 1 .

Escreva, para cada caso, a lei de velocidade para perda de A.

Passo 1

Vamos pra mais uma galeraaa!

Na letra a sabemos que a velocidade de reação é proporcional à sua concentração, elevada ao seu coeficiente.

Como na letra a o coeficiente é 2, teremos:

T a x a ∝ A 2

Ou podemos igualar essa proporção quando adicionamos a constante:

T a x a = k A 2

Para achar a constante, k, podemos usar a equação:

ln ⁡ [ A ] t = ln ⁡ [ A ] 0 - k t

Reorganizando:

k = 1 t ln ⁡ A 0 A t

O problema nos disse que:

[ A ] t = A 0 4

t = 61   m i n

Substituindo:

k = 1 61   m i n ln ⁡ 4 = 0,023   m i n - 1

Na taxa:

T a x a = ( 0,023   m i n - 1 ) A 2

Passo 2

Na letra b nós temos inicialmente a situação abaixo:

Após 45 segundo são formados 0,00125 mol/L de reagente:

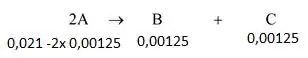
Então:

[ A ] 0 =   0,021   m o l · L - 1

[ A ] t = 0,021 - 2 × 0,00125 m o l · L - 1 = 0,019   m o l · L - 1

Achando a constante:

k = 1 45   s ln ⁡ 0,021   m o l · L - 1 0,019   m o l · L - 1 = 2,2 × 10 - 3   s - 1

E nossa velocidade ficara como:

T a x a = ( 2,2 × 10 - 3   s - 1 ) A 2

Passo 3

Vamos para o fim da questão !!

Na situação inicial temos:

Após 10,8 min:

Se:

3 x = 0,04 → x = 0,04 3

Então:

[ A ] 0 =   0,0 6   m o l · L - 1

[ A ] t = 0,021 - 2 × 0,04 3 m o l · L - 1 = 0,0 34   m o l · L - 1

Achando a constante:

k = 1 10,8   m i n ln ⁡ 0,0 6   m o l · L - 1 0,034   m o l · L - 1 = 5 , 2 × 10 - 2   m i n - 1

E nossa velocidade ficara como:

T a x a = ( 5,2 × 10 - 2   m i n - 1 ) A 2

E é isso ai!

Resposta

  1. T a x a = 0,023   m i n - 1 A 2 ;
  2. T a x a = 2,2 × 10 - 3   s - 1 A 2 ;
  3. T a x a = 5,2 × 10 - 2   m i n - 1 A 2 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14.25-A reação de decomposição do pentóxido de dinitrogênio, N 2 O 5 , é de primeira ordem com constante de velocidade igual a 3 * 10 - 5s - 1 , em 298 K. (a) Qual é a meia vida (em horas) de decompos
14.22- Na fermentação da cerveja, etanal, que tem o cheiro de maçãs verdes, é um intermediário na formação do etanol. O etanal se decompõe na seguinte reação de primeira ordem C H 3 C H O g → C H 4 g
14.28- A constante de velocidade de primeira ordem da fotodissociação de A é 6,85 * 10 - 2 min - 1 ⁡ . Calcule o tempo necessário para que a concentração de A caia até (a) 1 8 [ A 0 ] ;(b) 10 % do val
14.26-14.25-A reação de decomposição do pentóxido de dinitrogênio, N 2 O 5 , é de primeira ordem com constante de velocidade igual a 0,15s - 1 , em 353K . (a) Qual é a meia vida (em horas) de decompos
14.27- A meia vida da decomposição de primeira ordem de A é 355 s. Qual é o tempo necessário para que a concentração de A caia até (a) 1 8 [ A 0 ] ;(b) um quarto da concentração inicial; (c) 15 % da c