Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 6.Questões e Problemas - Ex. 13

O diâmetro interno de um tanque na forma de um cilindro aberto foi medido. Os resultados para quatro réplicas de medidas foram 5,4; 5,2; 5,5 e 5,2 m. As medidas da altura do tanque geraram os resultados 9,8; 9,9 e 9,6 m. Calcule o volume do tanque em litros e o desvio padrão para o resultado.

Passo 1

Oi galerinha, ansiosos para resolver este exercício? Então vem comigo.

Primeiramente precisamos relembrar a equação do volume do cilindro, que a gente aprendeu lá na escola:

V = π r 2 h

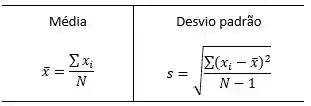
E as equações de média e desvio padrão:

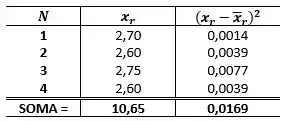
Agora nós temos 4 medidas do diâmetro, iremos dividir essas medidas por 2, para obtermos o raio e então iremos obter a média e o desvio padrão do raio ( x - r e s r ):

x - r = 10,65 4 = 2,66   m

s r = 0,0 169 4 - 1 = 0 , 08   m

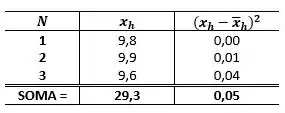
E temos três medidas para a altura do tanque, e também iremos fazer a média e o desvio padrão ( x - h e s h ):

x - h = 29,3 3 = 9,8   m

s h = 0,05 3 - 1 = 0,2   m

Passo 2

Voltando na nossa equação inicial, iremos obter o volume do cilindro em m 3 e queremos em litros ( L ), e sabemos que:

1   m 3 = 1000   L

Logo:

V = π ∙ 2,66 2   m 2 ∙ 9 , 8   m ∙ 1000   L 1   m 3

V = 2,2 ∙ 10 5   L

Passo 3

Porém ainda precisamos estimar o desvio padrão deste resultado e temos a equação:

V = π ∙ 2,66 ± 0,08   m 2   ∙ 9,8 ± 0,2   m

Primeiramente precisamos obter o desvio padrão da exponenciação:

y = a x = ( 2,66   m ) 2 = 7,08   m 2  

E o desvio padrão para esta relação:

s y = y ∙ x ∙ s a a = 7,08 ∙ 2 ∙ 0,08 2,66 = 0,4   m 2

Então agora temos:

V = π ∙ 7,08   ± 0,4   m 2   ∙ 9,8 ± 0,2   m

E precisamos calcular o desvio padrão de um produto:

y = a ∙ b = π ∙ 7,08   m 2 ∙ 9,8   m 1000   L 1   m 3 =   2,2 ∙ 10 5   L

s y = y ∙ s a a 2 + s b b 2 = 2,2 ∙ 10 5   L ∙ 0,4 7,08 2 + 0,2 9,8 2 = 2,2 ∙ 10 5   L ∙ 0,06  

s y = ±   0,1   L

Então nossa resposta será:

V = 2,2 ∙ 10 5   ± 0,1   L  

Até mais pessoal.

Resposta

V = 2,2 ∙ 10 5   ± 0,1   L .

Exercícios de Livros Relacionados

Cite três tipos de erros sistemáticos.
O método descrito no Problema 5-8 deve ser utilizado na análise de minérios que têm cerca de 1,2 % em ouro. Que massa mínima deve ter uma amostra se o erro relativo resultante da perda de 0,4 mg não p
Um método de análise gera massas de ouro que são mais baixas por um fator de 0,4 mg. Calcule o erro relativo porcentual provocado por essa incerteza se a massa de ouro na amostra for:(a) 700 mg.(b) 45
A mudança de cor de um indicador químico necessita de um volume adicional de 0,04 mL em uma titulação. Calcule o erro relativo porcentual se o volume total da titulação for:(a) 50,00 mL.(b) 10,0 mL.(c
Problema Desafiador. Os dados que seguem representam três conjuntos de dados para a massa atômica do antimônio obtidos a partir do trabalho de Willard e McAlpine:(g) Compare a média global dos 11 dado