Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 10.Problemas Teóricos - Ex. 22

A divisão dos feixes atômicos na experiência de Stern-Gerlach é pequena e se opera ou com grandes gradientes do campo magnético ou com ímãs compridos, para se obterem boas observações. Com um feixe de átomos de momento angular orbital nulo, como H ou Ag, o desvio é dado por x = ± μ B L 2 4 E K d B d z , em que μ B é o magnéton de Bohr (Problema 10.9), L é o comprimento do ímã, E K é a energia cinética média dos átomos do feixe, e d B / d z é o gradiente do campo magnético. (a) Com a distribuição de velocidades de Maxwell=Boltzmann, mostre que a energia cinética de transição média dos átomos que emergem num feixe através de orifício nas paredes de um forno, na temperatura T, é 2kT. (b) Calcule o gradiente de campo magnético capaz de provocar a separação de 1,0 mm num feixe de átomos de Ag provenientes de um forno a 1000 K, com um ímã de 50 cm de comprimento.

Passo 1

A distribuição de velocidade de um feixe molecular é relacionada a distribuição de velocidade dentro da câmara por um fator de ν c o s θ como mostrado na figura abaixo. Desde que a integração em torno de todo θ possível seja feita, o fator c o s θ pode ser absorvido dentro de uma constante de proporcionalidade.

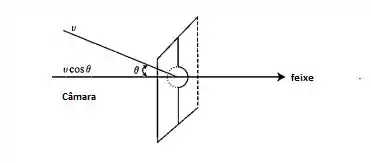
Passo 2

(a) Pela normalização em torno das velocidades possíveis do feixe molecular ( 0 < ν f e i x e < ∞ )

f f e i x e = C ν ν 2 e - m ν 2 2 k T = C ν 3 e - m ν 2 2 k T

∫ v = 0 ∞ f f e i x e   d v = 1 = C ∫ v = 0 ∞ v 3 e - m v 2 2 k T d v = C 1 2 m 2 k T 2

C = 2 m 2 k T 2

Passo 3

Agora vamos calcular a velocidade dada por:

< v 2 >   = ∫ v = 0 ∞ v 2 f f e i x e v d v = C ∫ v 5 e - m v 2 2 k T d v

= C 1 m 2 k T 3 = 2 m 2 k T 2 m 2 k T 3 = 4 k T m

< E k >   = m 2 < v 2 >   = m 2 4 k T m = 2 k T

Passo 4

(b) Agora vamos calcular a posição desse benditooo!!!

Δ x = 2 μ B L 2 4 E k d B d z

d B d z = 4 E k Δ x 2 μ B L 2 = 4 2 k T Δ x 2 μ B L 2 = 4 k T Δ x μ B L 2

Vamos agora substituir nossos valores:

d B d z = 4 1,3807 × 10 - 23 1000 1 × 10 - 3 9,27402 × 10 - 24 × 50 × 10 - 2

d B d z = 23,8   T m - 1

Resposta

d B d z = 23,8   T m - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um dos primeiros satélites lançados com sucesso pelos Estados Unidos na década de 1950 era essencialmente um grande balão esférico (aluminizado) de Mylar a partir do qual sinais de onda de rádio eram
Regulamentações exigem que as estações de rádio licenciadas limitem a potência de sua radiodifusão para evitar interferência com sinais de estações distantes. Você está encarregado de verificar a conf
Considere um dipolo elétrico irradiando que esteja ao longo do eixo z. Seja I 1 a intensidade da radiação a uma distância de 10 m e a um ângulo de 90°. Determine a intensidade (em termos de I 1 ) a (a
(a) Para a situação descrita no Problema 24, em que ângulo a intensidade a uma distância de 5.0m é igual a I 1 ? (b) A que distância a intensidade é igual a I 1 quando θ = 45 ° ?
Você e sua equipe de engenharia estão encarregados de estabelecer uma rede de telefonia sem fio para uma pequena aldeia em uma região montanhosa. A antena transmissora de uma estação é uma antena de d