- Faça o gráfico da função de onda da partícula em uma caixa para e .
- Quantos nodos tem a função de onda? Onde ocorrem esses nodos?
- Repita as partes (a) e (b) para .
- Que conclusão geral você pode tirar para a relação entre n e o número de nodos presentes em uma função de onda?
- Converta o gráfico para distribuição de densidade de probabilidade: em quais valores de x é mais provável encontrar a partícula?
- Repita a parte (e) para .
Passo 1
Legal galera, vamos descobrir como calculamos a função de onda de uma partícula, certo?
Como a função de onda está em função do seno, podemos assumir que ela irá apresentar o mesmo comportamento em intervalos definidos
Então, se substituirmos para e
Como x também é dada em m:
Lançando nos dados os valores de para valores de x indo de 0 até 1:
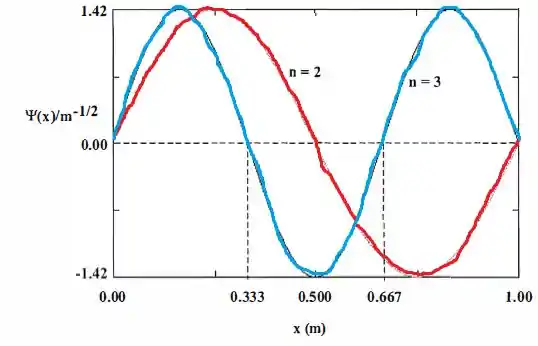
Passo 2
E se lembramos que os nodos são os valores de x cuja função de onda é zero:
Aplicando o arcoseno:
Então, para nós temos nódulo no ponto 0,5 m, já que os demais são os extremos.
Para a letra c:
Aplicando o arcoseno:
Então, para nós temos nódulo no ponto 0,333 m e 0,667 m.
Passo 3
E agora? Qual a relação entre n e o número de nodos presentes em uma função de onda?
Vamos analisar!
Quando e quando .
Então o que nós podemos concluir?
Que:
Tranquilo até aqui?
Passo 4
Bom galera, agora n[os precisamos da distribuição de densidade de probabilidade,
Substituindo para e
Lançando nos dados os valores de para valores de x indo de 0 até 1:
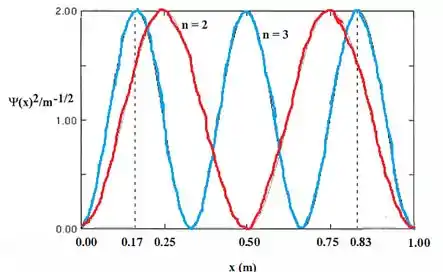
Com o gráfico nós já conseguimos responder onde a probabilidade de encontrar a partícula é maior.
Já sabem onde?
Nos picos, certo?
Então, para os picos estão localizados em e
E para os picos estão localizados em e
Então é isso! Finalizamos mais uma !!
Resposta
- e (c) :
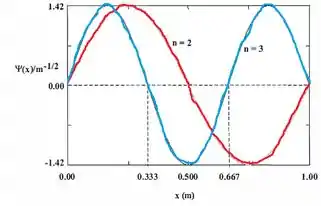
- e
- e