Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 17.1 - Ex. 51
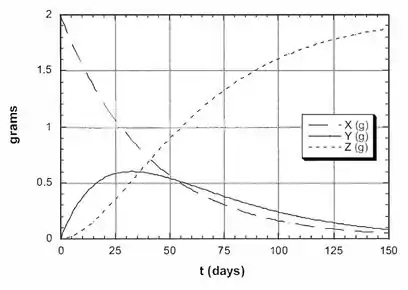
Um isótopo radioativo X, com meia vida de , decai a outro isótopo radioativo, Y, com meia vida de . Este último decai a um isótopo estável, Z. Estabeleça e resolva as leis de velocidade das quantidades dos dois nuclídeos em função do tempo e lance seus resultados como um gráfico.
Passo 1
Huuunm...
Esta não é tão molezinha assim !
Vamos com calma! Primeiro vamos ver o que acontece:
A taxa de reação quando X decai em Y é dada por:
Vamos reorganizar:
Se integrarmos:
Onde C é a constante, e para acha-la basta lembrarmos que, quando o :
Substituindo:
Aplicando o exponencial:
Isolando X:
Então, a quantidade de X é representada pela equação acima, quando o isótopo X decai em Y.
Tranquilo até aqui?
Passo 2
Para o Y nós teremos:
Reorganizando:
E substituindo o X do passo 1:
Fazendo o mesmo procedimento do passo 1 e lembrando que :
Então já achamos a equação para a concentração de Y
Passo 3
Agora só precisamos da concentração de Z.
Para isso precisamos lembrar que, no tempo
Substituindo os valores do passo 1 e 2:
Reorganizando:
Então:
Acharam que acabou? Ainda não !
Passo 4
Vamos achar as constantes de decaimento:
Como a meia vida para o X é
E para o Y é
E assumindo que:
Então as concentrações serão:
Usando estas equações e variando o tempo poderemos montar os gráficos:
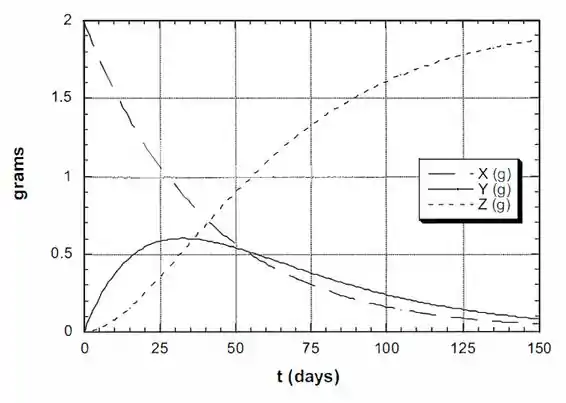
Um pouco cabulosa, não é?! Mas finalizamos mais uma !
Resposta
