Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 11.Problemas Numéricos - Ex. 15
15 – A teoria FEMO (Problema 11.14) de moléculas conjugadas é muito aproximada; melhores resultados são obtidos com a teoria simples de Hückel.
A) Para um polieno conjugado linear com cada um dos N átomos de carbono contribuindo com um elétron num orbital 2p, as energias Ek dos orbitais moleculares π resultantes são dadas por:
Use essa expressão para fazer uma estimativa empírica razoável da integral de ressonância β para a série homologa formada pelo eteno, butadieno, hexatrieno e octatetraeno, sabendo que a absorção no ultravioleta correspondente à transição π*
B) Calcule a energia de deslocalização π, do octatetraeno
Onde, Eπ é a energia total da ligação π, e N é o nº de elétrons π.
C) No contexto desse modelo de Hückel, os orbitais moleculares π são escritos como combinações lineares dos orbitais atômicos 2p do carbono. O coeficiente do j-ésimo orbital atômico no k-ésimo orbital molecular é dado por:
Determine os valores dos coeficientes de cada um dos seis orbitais 2p em cada um dos seis orbitais moleculares π do hexatrieno. Associe cada conjunto de coeficientes (isto é, cada orbital molecular) com um valor da energia calculada através da expressão dada na parte (a). Comente as tendências que relacionam a energia de um orbital molecular com sua “forma”, que pode ser inferida a partir das magnitudes e sinais dos coeficientes na combinação linear que descreve o orbital molecular.
Passo 1
A)
As transições ocorrem para os fótons cujas energias são iguais a diferença entre a energia entre o estado de energia mais alto ocupado do orbital e a energia do estado de mais baixo do orbital
Sendo N o nº de átomos de carbono, C, nestas espécies, então o nº de elétrons π é também N.
Estes N elétrons ocupam os primeiros N/2 orbitais, visto que em cada orbital temos 2 elétrons. Assim, o orbital de nº N/2 é o do HOMO e o orbital de nº 1+N/2 é o do LUMO.
Passo 2
Escrevendo a energia do fóton em termos do nº de onda, substituindo a energia dada com as equações identificadas para o HOMO e o LUMO dada no enunciado, temos que:
A energia do fóton é:
Onde, h é a constante de Planck, e c a velocidade da luz no vácuo:
Assim,
Isolando β
Passo 3
Calculando a integral de ressonância para cada molécula:
-Eteno (C2H4):
Aplicando os valores:
-Butadieno (C4H6):
Aplicando os valores:
-Hexatrieno (C6H8):
Aplicando os valores:
-Octatetraeno (C2H4):
Aplicando os valores:
Passo 4
B)
Para acharmos a energia de deslocalização, vamos usar a eq. dada no enunciado:
A energia total do sistema de elétrons π, Eπ, é a soma das energias dos orbitais ocupados, dado por
Sendo
Para o octatetraeno (C8H10):
Assim,
Podemos escrever o somatório como:
Passo 5
Resolvendo os somatórios:
Assim, a energia da ligação π é:
Passo 6
A energia de deslocalização será, então:
Como foi calculado no item (A):
Assim,
Passo 7
C)
Com o propósito de comparação, vamos expressar as energias do orbital, pegando a expressão do enunciado para Ek, da seguinte forma
Também pelo enunciado, os coeficientes são calculados por:
Como estamos fazendo os cálculos aqui neste item para o hexatrieno, C6H8, assim
Também serão 6 orbitais atômicos e 6 orbitais moleculares, consequentemente, para cada orbital atômico j, dado um orbital molecular k, teremos um coeficiente, e da mesma forma, para cada orbital molecular k, dado um orbital atômico j, teremos um coeficiente.
Assim, usando as expressões seguintes podemos calcular todos os coeficientes e comparar com as respectivas energias dos orbitais
Passo 8
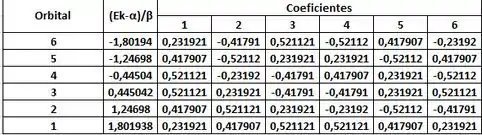
Calculando pelo EXCEL, obtém-se a seguinte tabela para os coeficientes:
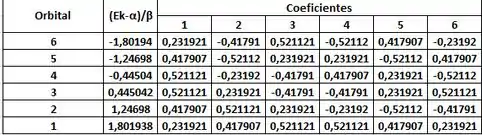
Pela tabela acima, você pode ver que a energia do orbital diminui, conforme o nº do orbital se eleva.
Resposta
A)
-Eteno (C2H4):
-Butadieno (C4H6):
-Hexatrieno (C6H8):
-Octatetraeno (C2H4):
B)
C)
