Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 7
Um método baseado em absorção atômica, desenvolvido para a determinação de ferro presente em óleo usado de motores a jato, apresentou um desvio padrão s 2,4 mg de Fe/mL, a partir de 30 análises realizadas em triplicata. Se s for uma boa estimativa de s, calcule os intervalos de confiança de 80% e 95% para o resultado 18,5 mg de Fe/mL, se estiver baseado (a) em uma única análise, (b) na média de duas análises e (c) na média de quatro análises.
Passo 1
Fala aí! Para resolvermos essa aqui, temos que lembrar da expressão usada para encontrar o intervalo de confiança para a média verdadeira:
Ali, z vai nos ajudar a encontrar o nível de confiança a partir da seguinte tabela:
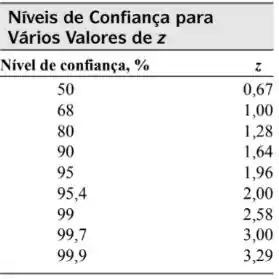
Com isso, podemos dar início aos nossos cálculos. Se liga, baseado em uma única análise, um intervalo de confiança de 80% para o resultado 18,5 de Fe/mL vai ser:
E para 95%:
Passo 2
Para os demais, vamos repetir o mesmo processo, mas dessa vez considerando um número maior de amostras. Olha só como vai ficar para duas análises:
E:
Passo 3
Por fim, vamos aplicar a equação para um total de 4 amostras:
E para 95% de confiança:
Resposta
(a)
(b)
(c)