Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 34b
Problema Desafiador. Os dados que seguem representam três conjuntos de dados para a massa atômica do antimônio obtidos a partir do trabalho de Willard e McAlpine:
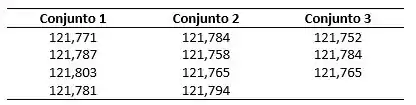
(b) Estabeleça os intervalos de confiança para 95% para cada conjunto de dados.
Passo 1
Oi galerinha, vem comigo resolver este exercício.
Queremos estabelecer os intervalos de confiança () para 95% para cada conjunto de dados, para isso iremos utilizar a equação:
Do item (a) temos:
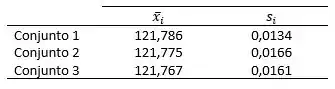
Passo 2
Para os Conjuntos 1 e 2, temos graus de liberdade, então:
O intervalo de confiança para o Conjunto 1:
E para o Conjunto 2:
Passo 3
O Conjunto 3 apresenta 2 graus de liberdade, logo:
Por fim, temos o intervalo de confiança para o Conjunto 3:
E ai pessoal, consegui ajudar? Espero que sim! Até mais.
Resposta
;
;
.
Exercícios de Livros Relacionados
Um método baseado em absorção atômica, desenvolvido para a determinação de cobre em combustíveis, gerou um desvio padrão combinado scomb 0,32 mg de Cu/Ml (s S s). A análise do óleo do motor de uma aer
Um método baseado em absorção atômica, desenvolvido para a determinação de ferro presente em óleo usado de motores a jato, apresentou um desvio padrão s 2,4 mg de Fe/mL, a partir de 30 análises realiz
Um método padrão usado na determinação de glicose em soro sangüíneo apresenta um desvio padrão de 0,40 mg/dL. Se s 0,40 mg/dL for uma boa estimativa de s, quantas réplicas de determinações deveriam se
Considere os seguintes conjuntos de réplicas de medidas:Calcule a média e o desvio padrão para cada um dos seis conjuntos de dados. Calcule o intervalo de confiança de 95% para cada conjunto de dados.
Antes de concordar com a compra de uma grande quantidade de solvente, uma companhia quer ter evidências conclusivas de que o valor médio para a concentração de uma determinada impureza é menor que 1 p