Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 9.Problemas Numéricos - Ex. 5

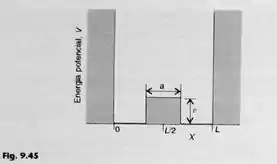
Um pequeno degrau na energia potencial é introduzido no problema de uma partícula numa caixa unidimensional, conforme pode ser visto na Fig. 9.45. (a) Escreva uma expressão geral para a correção de primeira ordem para a energia no estado fundamental, E 0 1 . (b) Calcule a correção de energia para a = L / 10   (assim, o pique no potencial ocupa os 10% centrais da caixa), com π = 1 .

Passo 1

Simbora!

Para bolar uma expressão para a correção, teremos que:

H 1 = 0   p a r a   0 ≤ x ≤ 1 2 L - a   e   1 2 L + a ≤ x ≤ L ϵ   p a r a   1 2 L - a ≤ x ≤ 1 2 L + a

Para a correção de primeira ordem, teremos:

E 1 1 = ∫ 0 L ψ 1 0 * H 1 ψ 1 0 d x = ∫ 1 2 L - a 1 2 L + a 2 L 1 2 sen ⁡ π x L ϵ 2 L 1 2 sen ⁡ π x L d x

Resolvendo,

E 1 1 = ϵ a L - ϵ π cos ⁡ π L + a 2 L sen ⁡ π L + a 2 L + ϵ π cos ⁡ π L - a 2 L sen ⁡ π L - a 2 L

Utilizando identidades trigonométricas, podemos simplificar essa equação, tendo então que:

E 1 1 = ϵ a L + ϵ π sen ⁡ π a L

Passo 2

Para a = L 10 , teremos:

E 1 1 = ϵ 10 + ϵ π sen ⁡ π 10 = 0,1984 ϵ

Resposta

  1. E 1 1 = ϵ a L + ϵ π sen ⁡ π a L
  2. 0,1984 ϵ
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma caixa unidimensional está no eixo x na região de 0 ≤ x ≤ L. Uma partícula nesta caixa está em seu estado fundamental. Calcule a probabilidade de a partícula ser encontrada na região (a) x L21 0
Uma partícula em uma caixa unidimensional com comprimento L está no primeiro estado excitado (n = 2). (A caixa tem uma extremidade na origem e a outra extremidade no eixo x positivo.) (A) Esboço ψ 2 (
Uma partícula de massa m tem uma função de onda dada por ψ x = A e - x a , onde A e a são constantes positivas. (a) Encontre a constante de normalização A. (b) Calcule a probabilidade de encontrar a p