Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 34d
Problema Desafiador. Os dados que seguem representam três conjuntos de dados para a massa atômica do antimônio obtidos a partir do trabalho de Willard e McAlpine:
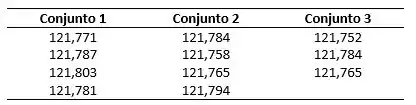
(d) Use o teste para determinar se a média dos dados do conjunto 3 é idêntica àquela do conjunto 1 em um nível de confiança de 95%.
Passo 1
Oi galerinha, vem comigo resolver este exercício.
Do item (a) temos:
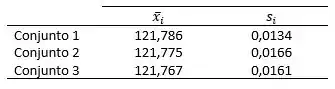
O teste estatístico é determinado por:
Onde:
Logo:
O valor crítico de para graus de liberdade, em um nível de confiança de 95% é:
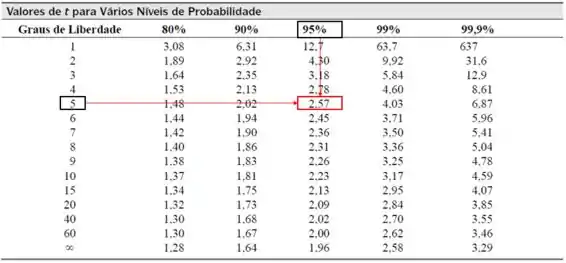
Como , não há diferença significativa para um nível de confiança de 95%
Até mais pessoal.
Resposta
Não há diferença significativa entre a média dos dados do conjunto 3 e o conjunto 1 para um nível de confiança de 95%.
Exercícios de Livros Relacionados
Descreva com suas próprias palavras por que o intervalo de confiança em relação à média de cinco medidas é menor que aquele para um único resultado.
Discuta como a dimensão do intervalo de confiança da média é influenciada pelos seguintes aspectos (todos os outros fatores são constantes):(a) O tamanho N da amostra.(b) O nível de confiança.(c) O de
Considerando um grande número de medidas de forma que s seja uma boa estimativa de e, determine que nível de confiança foi usado para cada um dos intervalos de confiança.
O último resultado de cada conjunto de dados do Problema 7-4 pode ser um valor anômalo. Aplique o teste Q (nível de confiança de 95%) para determinar se há ou não base estatística para a rejeição.
Dois métodos analíticos diferentes foram usados para determinar cloro residual em efluentes de esgoto. Ambos os métodos foram usados nas mesmas amostras, mas cada amostra foi coletada de vários locais