Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 1.1 - Ex. 58
Quantos elétrons podem ocupar uma subcamada com igual a (a) 0; (b) 1; (c) 2; (d) 3
Passo 1
Aqui, precisamos relembrar que é o número quântico azimutal, ou número quântico secundário, ou ainda número quântico de momento angular. Ele vai nos indicar o tipo de orbital que uma determinada subcamada possui – independente do número quântico principal n da subcamada – por intermédio de um número. Como são apenas 4 orbitais, eles serão identificados como 0, 1, 2 e 3, a partir da seguinte tabela:
Passo 2
Depois que identificamos cada orbital pelo seu número quântico secundário, , precisaremos também relembrar quantos orbitais uma subcamada pode comportar – e isso vai depender justamente do tipo de orbital dessa subcamada.
Relembraremos, também, que cada orbital, representado por uma “casinha” pode comportar até no máximo 2 elétrons. Dessa forma, seremos capazes de responder ao exercício com a tabela seguinte:
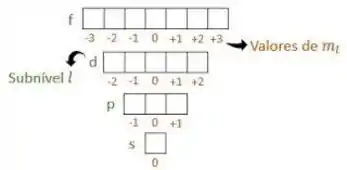
(a) Sendo 0, isso corresponde aos orbitais do tipo s, que comporta apenas até 2 elétrons
(b) Sendo 1, isso corresponde aos orbitais do tipo p, que comportam até 6 elétrons.
(c) Sendo 2, isso corresponde aos orbitais do tipo d, que comportam até 10 elétrons.
(d) Sendo 3, isso corresponde aos orbitais do tipo f, que comportam até 14 elétrons
Resposta
(a) Até 2 elétrons
(b) Até 6 elétrons
(c) Até 10 elétrons
(d) Até 14 elétrons