Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 4.1 - Ex. 114
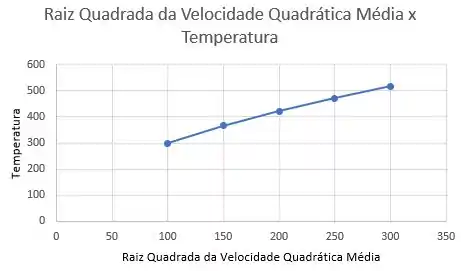
Como a raiz quadrada da velocidade quadrática média das moléculas de um gás varia com a temperatura: Ilustra esta relação lançando em gráfico a raiz quadrada da velocidade quadrática média das moléculas de N2 contra a temperatura de T = 100K a T = 300K.
Passo 1
A equação da velocidade média das raízes das moléculas de gás é:
Tendo que:
Massa Molar do (devemos passar para kg.mol-1);
Temperatura variando de 100 K a 300 K.
Podemos fazer uma tabela com a velocidade variando a cada 50 K:
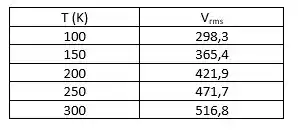
Passo 2
A partir da tabela desenvolvida, jogando os valores no Excel, obtemos o seguinte gráfico que relaciona a raiz quadrada da velocidade quadrática média das moléculas de N2 com a temperatura de a :
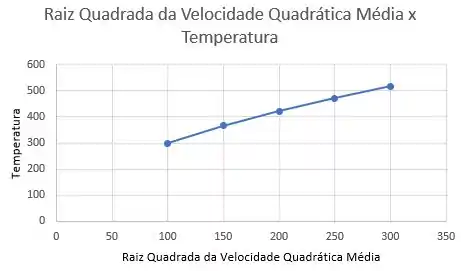
Resposta
Exercícios de Livros Relacionados
85. (a) A partir do gráfico da distribuição de velocidades de Maxwell mostrado na figura 4.27 , encontre o ponto que representa a velocidade mais provável das moléculas. (b) O que acontece com a perce
78. Calcule a energia cinética molar (em joules por mol) de uma amostra de gás neônio em (a) 25,0° C e (b) 26,0° C . (c) A diferença de energia molar entre as respostas (a) e (b) é a energia por mol n
80. Calcule as raízes quadradas das velocidades quadrática médias das moléculas de (a) gás fluor, (b) gás cloro e (c) gás bromo, todas em 350° C .
79. Calcule as raízes quadradas das velocidades quadrática médias das moléculas de (a) metano, (b) etano e (c) propano, todas em - 20° C .
81. A raiz quadrada das velocidades quadráticas médias das moléculas do gás metano, C H 4 , em uma dada temperatura, é 550m / s . Qual a raiz quadrática das velocidades quadráticas médias dos átomos d