Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 11.Problemas Numéricos - Ex. 5

5 – Repita o cálculo do Problema 11.4, porém fazendo o gráfico das densidades de probabilidade dos dois orbitais. Depois, forme a densidade diferença, isto é, a diferença entre ψ2 e 0,5{ψ2A + ψ2B}.

Passo 1

Vamos começar definindo as densidades eletrônicas de que podem ser escritas como:

ρ + = ψ + 2

ρ - = ψ - 2

Como foi dado no problema 11.4:

ψ ± = N ± 1 π a 0 3 0,5 e - z a 0 ± e - z - R a 0  

Onde,

N + = 1 2 1 + S 0,5

N - = 1 2 1 - S 0,5

Passo 2

Sendo S = 0,586, assim:

N + = 1 2 1 + 0,586 0,5 = 0,561

N - = 1 2 1 - 0,586 0,5 1,099

Consequentemente:

ρ ± = ψ ± 2 = N ± 2 1 π a 0 3 e - z a 0 ± e - z - R a 0 2

Onde, a0 é o raio de Bohr dado por:

a 0 = 52,9   p m

Assim, substituindo os valores de N+, N-, e a0:

ρ + = 1 1216 2 p m 3 e - z a 0 + e - z - R a 0 2

ρ - = 1 621 2 p m 3 e - z a 0 - e - z - R a 0 2

Passo 3

A densidade atômica é:

ρ = 1 2 ψ 1 s A 2 + ψ 1 s B 2

ρ = 1 2 1 π a 0 3 e - 2 r A a 0 + e - 2 r B a 0

Substituindo o valor:

ρ = 1 9,30 x 10 5 p m 3 e - 2 r A a 0 + e - 2 r B a 0

ρ = 1 9,30 x 10 5 p m 3 e - z a 0 + e - z - R a 0

A diferença de densidade é:

δ ρ ± = ρ ± - ρ

Passo 4

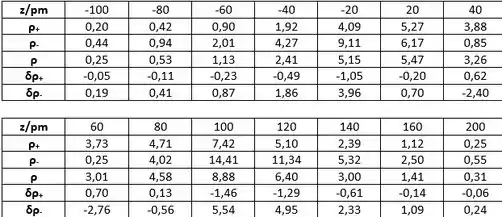
Com as informações do problema 11.4, e com as eq’s para as densidades e para a diferença de densidades, podemos montar a seguinte tabela com os valores de ρ e a diferença de densidades para cada valor de z:

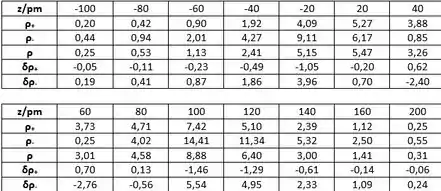
Passo 5

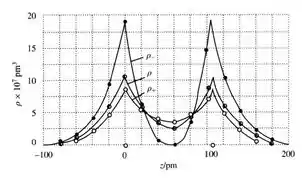
Com os dados da tabela, podemos plotar o gráfico para as densidades:

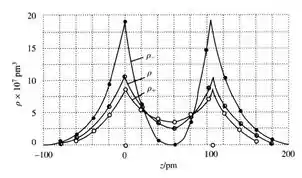
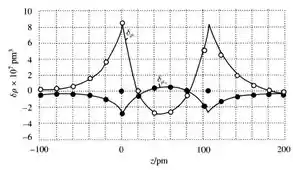
O gráfico para a diferença de densidades é:

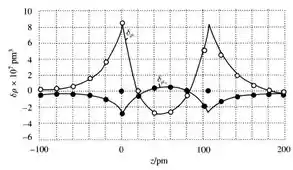
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9a – Dê os elementos de simetria das seguintes moléculas e identifique o grupo de simetria a que pertencem: a) NO2, b) N2O, c) CHCl3, d) CH2=CH2, e) cis-CHBr=CHBr, f) trans-CHBr=CHBr.
3 – O grupo D2h tem um eixo C2 perpendicular ao eixo principal e um plano de simetria especular horizontal. Mostre que o grupo tem, necessariamente, um centro de inversão.
5 – Verifique que a componente z do momento angular orbital é uma base para a representação irredutível de simetria A2 no grupo C3v.
1 – Dê os elementos de simetria das seguintes moléculas e identifique o grupo de simetria a que cada um pertence:A) CH3CH3 na conformação escalonada;B) cicloexano na conformação cadeira e bote;C) B2H6
Imagine que a molécula de metano seja distorcida (a) pelo alongamento de uma das ligações, ficando com simetria do C 3 v , e (b) pela abertura de um ângulo de fechamento de outro, ficando com a simetr