23 – Use um software matemático para construir a superposição de funções cosseno e mostre que a função de onda fica mias localizada à medida que aumenta o nº de componentes. Determine a probabilidade de ser observado um certo momento linear. Para fazer o gráfico da superposição, localize x = 0 no centro da tela e calcule a superposição nessa região. Calcule a localização média quadrática do pacote de onda, isto é, de 0,5.

Resolvendo pelo Mathcad nós vamos achar que:

Analisando o resultado obtido, quando n é um nº inteiro par, a função sen(0,5nπ) será igual a zero para todo n inteiro e par. Da mesma forma, quando n é nº inteiro e ímpar, a função cos(0,5nπ) será igual a zero para todo n inteiro e ímpar. Consequentemente, quando n é um nº inteiro, a integral anterior será igual

Logo, a cte de normalização será:

Assim, a função normalizada é

Considerando que a função cosseno seja ortogonal, assim o pacote de funções de onda, ψ (m, x), terá uma constante de normalização de

Assim,

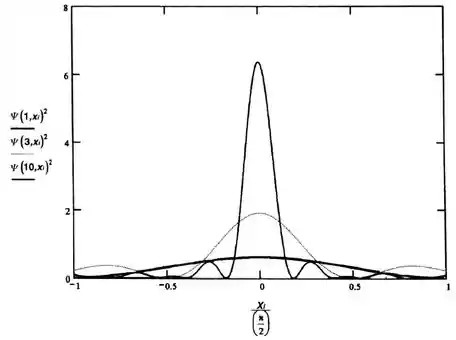
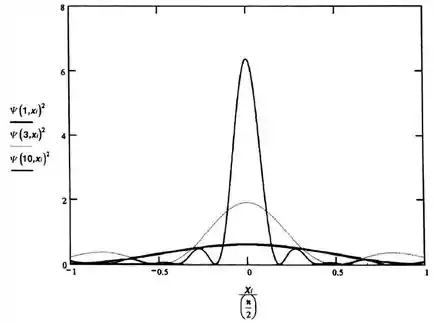
Plotando o pacote de ondas pelo Mathcad:

Vamos analisar o gráfico anterior :

Quando a superposição tem poucos termos, a posição da partícula é mal definida. Existe uma grande incerteza no conhecimento da posição da partícula. No entanto, quando muitos termos são adicionados para a superposição, a incerteza se estreita para uma pequena região próxima de x = 0. Para valores de m maiores do que 10 pode confirmar esta conclusão.

Cada função na superposição tem sido assimilada em igual peso para a constante de normalização (1/m)0,5. Isto significa que cada função cosseno na superposição tem uma probabilidade de contribuição idêntica no valor esperado para o momento. Cada função cosseno contribui com uma probabilidade igual a 1/m.

Além disso, cada função cosseno representa um momento da partícula que é proporcional ao argumento n porque o componente diferencial do quadrado do operador momento é proporcional a n.