Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 17.1 - Ex. 52
Suponha que o nuclídeo Y do Exercício 17.51 é necessário para pesquisa médica e que 2,00 g de nuclídeo X sejam fornecidos no . Em que momento Y será mais abundante na amostra?
Passo 1
Legal galera! Pelo Exercício anterior sabemos que a concentração de Y é dada por:
Para saber o valor do tempo onde a concentração é máxima podemos derivar a função e igualar à zero.
Para derivar podemos usar a regra da cadeia:
Aplicamos o ln:
Então:
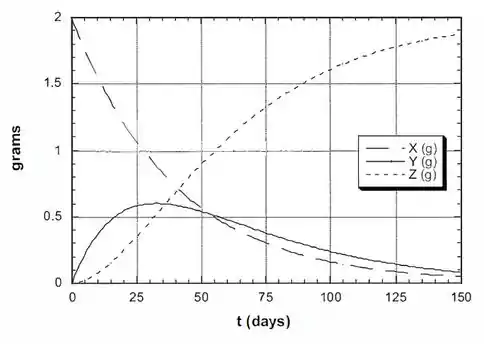
Podemos observar no gráfico do exercício anterior que nosso resultado bate com o que foi descoberto:
Prontinho !
Resposta
Exercícios de Livros Relacionados
Estabeleça quais dos seguintes decaimentos ou reações violam uma ou mais leis de conservação, e dar a lei ou leis violadas em cada caso: p + → n + e + + ν - e n → p + + π - e + + e - → γ p + + p - → γ
Um exemplo da situação discutida no problema 73 , é o do isótopo radioativo T h 239 , um emissor de α com uma meia vida de 7300 a n o s . Seu filho, R a 225 , é um emissor β , com meia vida de 14,8 d
Suponha que o isótopo A decai para o isótopo B e tem uma constante de decaimento λ A , e o isótopo B , por sua vez, decai, e tem uma constante de decaimento λ B . Deduza uma expressão para o tempo em
Determine a variação na estranheza em cada reação que segue, e diga se o decaimento pode ocorrer pela interação forte, ou pela interação fraca, ou não pode ocorrer. Ω - → Λ 0 + K - Ξ 0 → p + π -
Determine a variação na estranheza em cada reação que segue, e diga se o decaimento pode ocorrer pela interação forte, ou pela interação fraca, ou não pode ocorrer. Ω - → Λ 0 + ν e - + e - Σ + → p + π