Entalpia: Fenômenos Químicos
Produzido por Juliana EcheniqueTeoria
Reações endotérmicas e exotérmicas
Essa classificação tem a ver com o calor envolvido na reação! Mas se acalma, que é só uma classificação mesmo. Vem comigo 😊
Vamos pegar um exemplo de reação:
Essa reação, se feita à pressão constante, libera 208 KJ de calor para o meio. Ou seja, a entalpia do sistema diminui 208 KJ! Podemos escrever, então, que:
Uma reação que libera calor para o meio, ou seja, que tem é uma reação exotérmica!
A reação que faz o contrário, ou seja, retira calor do meio, ganhando calor, tem uma variação de entalpia positiva, já que sua entalpia aumenta.
Esse tipo de reação, com é chamada reação endotérmica!
Ou seja...

Entalpia de reação
Cada reação química tem uma energia envolvida, a entalpia de reação, representada por Essa energia representa o fluxo de calor necessário para que a reação ocorra. E o sinal de nos diz se esse calor é retirado ou cedido para o meio, ou seja, se a reação é endo ou exotérmica.
Antes de mais nada, vamos considerar algumas coisas:
- O de reação quase sempre é expresso depois dos produtos, ao final da reação:
- A entalpia de reação, assim como o depende da quantidade de reagente envolvida!
- Se a gente inverter a equação, a gente inverte o sinal do Ou seja,
Por exemplo, na reação:
A entalpia de reação é a entalpia necessária para que 1 mol de reaja com mols de . Se essa quantidade dobrar, por exemplo, o também dobra!
Podemos definir que
Entalpia padrão de reação
A entalpia de reação depende de algumas condições, como a pressão! O estado padrão de uma substância nada mais é que a substância em sua forma pura em 1 bar (e normalmente a )! Por exemplo: gelo no estado padrão é gelo puro sob 1 bar, água no estado padrão é água pura sob 1 bar...
A gente representa a entalpia padrão de reação por !
Ou seja, quando você ver só quer dizer que são as substâncias puras em pressão de 1 bar que estão reagindo!
Equações em várias etapas: lei de Hess
A gente já viu que a entalpia é uma função de estado, ou seja: só depende do estado final e inicial, né? Em reações que tem muitas etapas, calculamos o de reação a partir da lei de Hess, que diz:
A entalpia total da reação é a soma das entalpias em que a reação pode ser dividida.
Vamos ver um exemplo!
A reação:
Pode ser escrita em duas etapas:
Se somarmos as duas equações, e seus :
Voltamos à primeira reação.
Vale reparar aqui que quando somamos as duas etapas, a que é um intermediário da reação, some da reação global! Isso porque seria redundante escrever ela dos dois lados da equação, então é como se a gente “subtraísse” de cada um dos lados da equação!
Quando somamos as 2 etapas, achamos a primeira equação! Ou seja, o
Entalpia de formação
Além de somar as entalpias das etapas, outro jeito de calcular a entalpia de uma reação é à partir da entalpia padrão de formação dos reagentes, representada por
Vamos ver um exemplo:
A doé (já que é formado 1 mol de )!
A entalpia de formação de uma substância pode ser definida como a entalpia de uma reação que forma 1 mol da substância a partir de seus elementos na sua forma mais estável!
E como a gente sabe se os elementos estão na forma mais estável deles?
Isso vem com a prática, mas a forma mais estável de um componente é a forma que ele aparece com maior frequência na natureza! Por exemplo: a forma mais estável do carbono é o grafite, e não o diamante; a forma mais estável do oxigênio é o , e não o ...
A de um elemento na sua forma mais estável é zero!
E como a gente usa as entalpias de formação para calcular a entalpia da reação?
Onde são os coeficientes estequiométricos de cada componente.
Ou seja, a gente calcula as entalpias de formação dos produtos e subtrai a dos reagentes!
Entalpia de ligação
Os átomos se ligam com o intuito de se estabilizar, não é? Se pensarmos em uma reação do tipo:
Vemos que, para separar a ligação entre os dois s da molécula de , é necessário ceder energia para o sistema!
Isso porque estamos pegando os dois átomos (que se juntaram para se estabilizar) e desestabilizando eles de novo ahah O que você tem que lembrar dessa história é que para quebrar ligações, precisamos ceder calor ao sistema!
Já para formar ligações, o sistema vai liberar calor, ou seja:
Ou seja: a formação de ligações vai ser sempre exotérmica ( e a quebra das ligações, sempre endotérmica (!
Para calcular o de uma reação em que ligações são quebradas nos reagentes e formadas no produto, fazemos:
Poréeem, como a entalpia das ligações dos produtos vai ser negativa (já que são ligações formadas e, portanto, exotérmicas) e a dos reagentes positivas, podemos escrever:
Recapitulando...
Nós temos 3 formas de calcular a entalpia de uma reação:
1. Pela entalpia de formação de seus reagentes e produtos:
E temos que lembrar que a entalpia de formação de substâncias puras em sua forma mais estável é sempre 0!
2. Pela entalpia de ligação das ligações formadas e quebradas pela reação:
3. Se ela tiver muitas etapas, somamos as entalpias de cada uma das etapas! (Lei de Hess):
Vamos fazer uns exercícios pra aplicar esse mooonte de coisa? 😊
Entalpia de reação
Entalpia padrão de reação
Equações em várias etapas: lei de Hess
Entalpia de formação
Entalpia de ligação
Recapitulando...
Exercícios Resolvidos
Exercício Resolvido #1
BROWN, Theodore; LEMAY, H. Eugene; BURSTEN, Bruce E. Química: a ciência central. 9 ed.Prentice-Hall, 2005, Exercício 5.33
Considere a seguinte reação:
a) A reação é endotérmica ou exotérmica?
b) Calcule a quantidade de calor transferida quando 2,4g de Mg(s) reagem a pressão constante.
c) Quantos gramas de MgO são produzidos durante uma variação de entalpia de
d) Quantos de calor são absorvidos quando se decompõem em a pressão constante?
Passo 1
a) Como o podemos concluir que a reação é exotérmica e libera calor pro ambiente!
Passo 2
b) A proporção entre (calor envolvido) é:
Como a massa molar do é 24g...
A quantidade de calor transferida quando 2,4g de Mg(s) reagem é, portanto, 60,2 kJ.
Passo 3
c) A relação entre calor envolvido na reação e MgO é:
Como a massa molar de MgO (s) é 40g, podemos escrever essa relação como:
Ou seja, 6,38g de MgO(s) são produzidos com 96kJ de calor trocado.
Passo 4
d) Se queremos saber a entalpia de decomposição do MgO(s), precisamos pegar a reação no sentido inverso:
A proporção continua a mesma entre MgO (s) e calor envolvido (até porque vamos lembrar que )... A diferença é que, se no sentido direto a reação era exotérmica e liberava calor, no sentido inverso ela vai absorver calor!
A reação precisa absorver 112,9kJ para que 7,5g de MgO se dissolvam!
Resposta
a) A reação é exotérmica.
b)
c)
d)
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp282-Exercício 7.43
O dissulfeto de carbono pode ser preparado a partir do coque (uma forma impura de carbono) e do enxofre elementar:
a) Qual é o calor absorvido na reação de 1,25 mol de
b) Calcule o calor absorvido na reação de 197g de carbono com excesso de enxofre.
c) Se o calor absorvido na reação foi 415kJ, quanto foi produzido?
Passo 1
a) Essa questão é de novo só estequeometria!
A relação entre o e o calor absorvido na reação é:
Passo 2
b) A relação entre o carbono e o calor absorvido na reação é:
Como a massa molar do C é 12g..
Passo 3
c) Para cada 358,8 kJ absorvido pelos reagentes, 4 mols de são produzidos...
Resposta
a)
b)
c)
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp283-Exercício 7.61
O metal bário é produzido pela reação do metal alumínio com óxido de bário.
Calcule, a partir das entalpia padrão de reação, a entalpia para a produção do metal bário na reação:
Passo 1
Temos duas reações, temos a entalpia delas, e percebemos que mexendo um pouco nelas e somando as duas conseguimos chegar na terceira! Tudo isso são indícios que vamos usar a lei de Hess!
Vamos por partes: precisamos arrumar as duas equações de um jeito que, somando elas, consigamos chegar na terceira! Para isso, é só você procurar os reagentes da terceira reação nas reações de cima...
Como o é um reagente na terceira e um produto na primeira reação, precisamos inverter essa primeira reação! Quando invertemos ela, o sinal do também muda:
Vai virar...
Quanto à segunda, como o é reagente nas duas reações, deixamos ela assim mesmo!
Passo 2
Agora vamos tentar somar as duas equações:
Agora temos um problema diferente: o Como o é formado na primeira reação e consumido na segunda, o jeito mais certo de chegar na reação global é igualando sua quantidade nas duas equaçoeS. Assim, fazemos com tudo que foi produzido na etapa seja consumido na segunda, e aí ele não aparece na terceira reação, que é a reação global
Para igualar as quantidades, precisamos multiplicar a primeira reação por : toda a reação, inclusive o
Passo 3
Agora só basta somar!
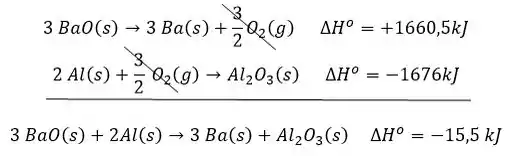
Assim, a entalpia para produção do é -15,5kJ
Resposta
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp283-Exercício 7.63
Determine a entalpia da reação de hidrogenação do etino e do etano:
À partir dos seguintes dados:
Passo 1
Vamos lembrar que, para calcular a entalpia de uma reação à partir das entalpias de formação dos reagentes e produtos basta fazer:
Vamos por partes!
Para calcular nesse caso, fazemos:
Já para os reagentes:
Passo 2
Assim, substituindo na fórmula...
Resposta
Exercício Resolvido #5
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp283-Exercício 7.83
Use as entalpias de ligação das tabelas abaixo para estimar a entalpia de reação de:
a)
b)
c)
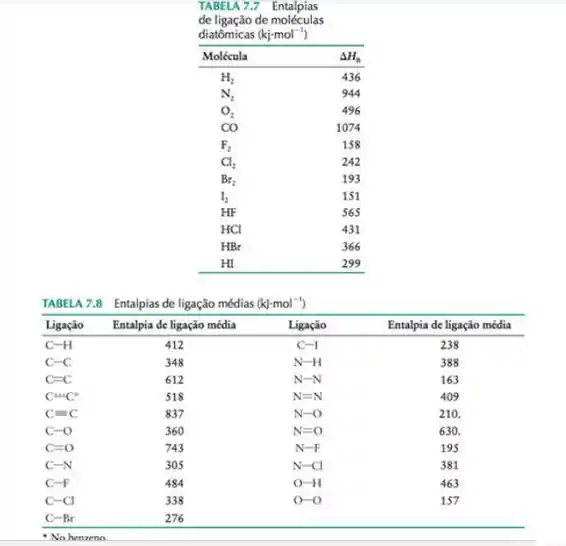
Passo 1
Para analisar a entalpia de reação a partir das entalpias de ligação, precisamos analisar todas as ligações que vão ser quebradas nos reagentes e todas que vão ser formadas nos produtos, para depois fazer a conta:
Então vamos por partes:
a)
Nos reagentes (ligações que vão ser quebradas), temos:
Nos produtos (ligações que vão ser formadas), temos:
OBS: Se você usar a fórmula , a própria fórmula já inclui quem é exotérmico e quem é endotérmico, e, portanto, basta somar as energias de ligação sem ter que se ligar no sinal!
Passo 2
Agora vamos calcular:
Passo 3
b)
Vamos analisar as ligações dos produtos e dos reagentes:
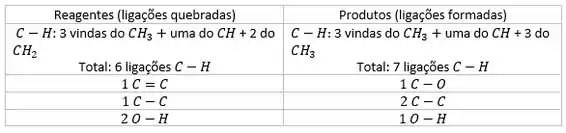
Fazendo as contas substituindo os valores das tabelas, achamos:
Para os reagentes (ligações quebradas):
Para os produtos (ligações formadas):
E, então:
Observação: Você vai ver, fazendo exercícios, que algumas ligações estão tanto nos reagentes quanto nos produtos, e quando contamos elas em ligações quebradas e em ligações formadas, é como se adicionássemos para depois retirar! Assim, faz muito mais sentido simplesmente contar as diferenças! Por exemplo, o quadro dessa questão podia ser:
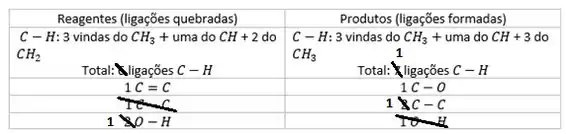
Ou seja:
A conta fica beeem mais fácil e dá o mesmo!
Passo 4
c)
Analisando as ligações:
Para os reagentes:
- 4
- 1
Para os produtos:
Eliminando o que aparece tanto nos produtos quanto nos reagentes, para não ter que somar e depois subtrair...
Assim,
Resposta
a)
b)
c)
Exercício Resolvido #6
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp283-Exercício 7.55
A entalpia de formação do trinitro-tolueno (TNT) é e a densidade, . Em princípio, ele poderia ser usado como combustível de foguetes, com os gases formados na decomposição saindo para dar o impulso necessário. Na prática, é claro, ele seria extremamente perigoso como combustível, porque é sensível ao choque. Explore seu potencial como combustível de foguete, calculando a densidade de entalpia (a entalpia liberada por litro) na reação:
Dados:
Passo 1
Como os dados são as entalpias de formação de duas das substâncias, vamos calcular o à partir dos
Vamos lembrar que, para fazer isso, precisamos calcular:
Começando pelos reagentes...
O porque é uma substância pura em sua forma mais estável. 😊
Para os produtos:
Assim,
Passo 2
Esse foi calculado para a queima de 4 mols de TNT!
Para calcularmos a entalpia liberada por litro, vamos precisar da massa molar e da densidade.
Ao mesmo tempo, temos a densidade, que diz que:
Ou seja, 1 litro de TNT tem 1650gramas! Para calcular o calor liberado por litro:
O calor liberado por litro de tolueno é, então, !
(Por mais que pareça um absurdo, é bem coerente com um explosivo, que precisa mesmo liberar muito calor na explosão ahahah)
Resposta
Exercício Resolvido #7
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp283-Exercício 7.65
Use as entalpias padrão de formação abaixo e calcule a entalpia padrão da reação do ácido nítrico puro com hidrazina:
Dados:
Passo 1
Para calcular a entalpia padrão de reação à partir das entalpias de formação de cada componente, vamos fazer:
Começando pelos reagentes, podemos calcular:
Já para os produtos...
Lembrando que, como o é uma substância pura na sua forma mais estável, sua entalpia de formação é 0!
Assim,
Resposta
Exercício Resolvido #8
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp283-Exercício 7.69
Calcule a entalpia de reação de síntese do gás brometo de hidrogênio, , a partir das seguintes informações:
Passo 1
Temos 3 reações e queremos chegar a uma reação global final. Vocês já sabem pra onde isso tá indo né?
Lei de Hess! Vamos manipular as três reações que nós temos para achar a reação final e depois somar as 3 (e suas respectivas entalpias) para achar a entalpia da reação global! 😊
A gente já sabe que precisa achar os reagentes da reação global, não é? Então primeiro, vamos organizar em cada etapa reacional se os reagentes e os produtos estão do lado certo!
Na já vemos que o está como reagente, sendo que na reação global ele é produto! Ou seja, precisamos inverter essa reação e pegar seu sentido inverso:
Não se esqueça que com isso a entalpia muda de sinal!
Passo 2
Para a e a é um pouco mais complicado, e a gente precisa ter bom senso!
As duas parecem estar certas, não é? Já que nas duas o é um reagente.. Mas, se somarmos elas do jeito que estão, teremos como reagente na reação global, e ele não é!
Ou seja: precisamos dar um jeito de cortar o do rolê!
Para fazer isso, vamos inverter a equação , assim, tudo que for formado de vai ser consumido na reação 3 e o não vai aparecer na reação global!
Daí agora você pode estar com duas dúvidas:
- Por que não inverter a reação 3?
- E o ele também não vai ser formado na etapa 2 e consumido na etapa 3?
Não invertemos a reação 3 porque, das 3 etapas, só ela tem o um dos reagentes da reação global!
É só a gente olhar pros coeficientes estequiométricos e perceber que a etapa 3 tem 1 mol a mais de como reagente do que a etapa 2 como produto. Assim, quando somarmos as duas, ainda vai sobrar do lado dos reagentes.
Ou seja, ficamos com:
Passo 3
Juntando as 3...
Para sumir com os intermediários de reação, precisamos multiplicar a primeira etapa por 2! Assim, podemos somar as 3 etapas e achar:
Tudo que estiver do lado dos produtos e dos reagentes vai ser cortado da reação global quando somarmos as 3 etapas:
Resposta
Exercício Resolvido #9
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp283-Exercício 7.71
Calcule a entalpia padrão de formação do pentóxido de dinitrogênio a partir dos seguintes dados:
E da entalpia padrão de formação do óxido nítrico,
Passo 1
Esse problema é bem inteligente, já que, quando a gente vê 2 reações, o instinto que a gente tem é somar as duas e tentar aplicar a lei de Hess, não é?
Mas não é por aí não! Ó: quando ele dá o da primeira reação e a entalpia padrão de formação do ele dá todos os dados que você precisa para calcular a
Com esse dado, a gente pode usar o da segunda reação e calcular a entalpia de formação do , já que a entalpia de formação do é 0.
Vamos com calma...
Primeiro, vamos usar a primeira equação para calcular a entalpia de formação do
Para a primeira equação isso dá:
Passo 2
Agora, usando a segunda equação, vamos achar o
Ou seja,
Substituindo valores: