Primeira lei da termodinâmica
Produzido por Juliana EcheniqueTeoria
Vamos falar sobre a primeira lei da termodinâmica? Vamos lá!
A primeira lei nos diz que:
“A soma do calor trocado por um sistema e do trabalho realizado por ou sobre um sistema é igual à variação da energia interna desse sistema.”

Essa frase aí tá cheia de conceitos que a gente precisa relembrar, né? Além disso, deu pra entender foi nada do que ela realmente quer dizer… Então…

Fala aí! Vamos bater um papo sobre a primeira lei da termodinâmica? Partiu!
Mas antes precisamos relembrar alguns conceitos básicos que vão nos ajudar a entender essa lei, belezinha?
Sistema
Nós vamos ver muito esse termo, então é importante saber o que realmente ele significa. Bom, sistema é uma porção do espaço que será considerada como nosso objeto de estudo. E aí tranquilo?
O limite desse sistema vamos chamar de fronteira, toda a região do espaço que faz fronteira com o sistema, chamaremos de vizinhança. Podemos demonstrar como algo assim olha só:
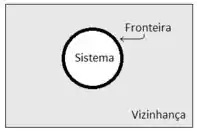
Esse nosso sisteminha também pode ser dividido em três tipos, em relação a trocas de matéria e energia, podem ser: sistemas abertos, que trocam massa e energia com a vizinhança, sistemas fechados, que trocam apenas energia com a vizinhança, e sistemas isolados, que não trocam nem massa nem energia com a vizinhança, tranquilo?
Trabalho
Bom, o trabalho é acordar cedo e ir… Brincadeirinha!
![]()
Trabalho aqui é uma interação onde uma força é aplicada produz movimento! Esse é aquele momento que a gente lembra dos bloquinhos sendo arrastado quando estudamos física, show?
Um exemplo de trabalho é a expansão de um gás que empurra um pistão. E como a gente pode calcular isso? Assim, olha só:
Esse aí é a quantidade infinitesimal de trabalho, a unidade dele é o Joule (J), o é uma pressão externa constante, a unidade dela é o Pascal (Pa) e o é uma variação infinitesimal no volume, e a unidade dele é o metro cúbico (m³), beleza?
Se a gente somar todas essas quantidades infinitesimais, vamos ter o seguinte:
Tranquilo?
Calor
O calor aqui é quando dois corpos com temperaturas diferentes são colocados em contato e ocorre a aproximação da temperatura dos dois. Tipo se colocarmos um cubinho de gelo no asfalto.
O calor pode ser calculado usando a temperatura, a massa e o calor específico do sistema , desse jeito aqui:
Mas também pode ser escrito usando a capacidade calorífica:
Show de bolinha!
Energia interna
A energia interna é literalmente algo que vem de dentro!
Ela é a soma de todos os vários tipos de energia que atuam em um sistema.
Ela varia quando calor é cedido ou retirado do sistema e também quando trabalho é feito pelo ou sobre o sistema… Opa! Então ela depende das duas quantidades que acabamos de ver, beleza?
Agora simmm... temos munição suficiente para atacar a primeira lei da termodinâmica, então vamos nessa!
Primeira lei da termodinâmica
Ao pé da letra a primeira lei da termodinâmica é exatamente aquilo que lemos lá em cima, mas ela pode ser interpretada da seguinte forma: a energia interna de um sistema isolado é conservada!
E o que isso significa pra gente matematicamente?
Isso aqui:
Essa equaçãozinha mostra pra gente que a variação da energia interna de um sistema isolado é igual à energia que passa, em forma de calor e trabalho, através das suas fronteiras.
Mas e nos casos dos sistemas abertos? Não podemos considerar a primeira lei da termodinâmica?
A primeira lei em um sistema aberto
Sim! A primeira lei também pode ser aplicada em situações com fluxo de matéria. Mas nesse caso, ela fica um pouco diferente, porque se existe um acúmulo de matéria também teremos um acúmulo de energia interna.
A variação de energia interna, nesse caso, será dependente de outro conceito, mas que não é novo pra gente, a entalpia. Podemos expressar ela assim:
Mas relaxa! Essa parte é beemmm menos comum de se encontrar e de aparecer nas provas, mas é importante a gente saber que existe, beleza?!
E aí, partiu reforçar nosso conhecimento com questõezinhas? Vamos lá!!
Sistema
Trabalho
Calor
Energia interna
Primeira lei da termodinâmica
A primeira lei em um sistema aberto
Exercícios Resolvidos
Exercício Resolvido #1
Apostila de fundamentos de Físico-Química - Universidade Federal de Sergipe
O volume de uma amostra de gás varia de 4,00 L para 6,00 L contra uma pressão externa de 1,50 atm e, simultaneamente, absorve 1000 J de calor. Qual é a variação na energia interna do sistema?
Passo 1
Fala aí! Partiu arrasar nesse assunto? Vamos lá!
Vamos começar anotando todos os dados do nosso enunciado, beleza?
Temos o seguinte:
E o exercício pede pra gente a variação de energia interna desse sistema… Vamos para as continhas!
![]()
Passo 2
O enunciado pede a variação da energia interna, e isso a gente sabe calcular por causa da primeira lei da termodinâmica, lembra dela?
Ela diz pra gente que:
Show! Já sabemos como calcular, só ta faltando achar o trabalho, então vamos achar ele!
Passo 3
A equação que ajuda a gente a calcular o trabalho é a seguinte:
Opa! temos todos os termos! Então vamos encontrar ele:
Olha o bizu aí! Esse trabalho tem que estar em Joules (J), precisamos converter esse resultado, vamos fazer assim:
Agora simmm!!
Passo 4
Partiu achar então a energia interna:
Show! Arrasamos!!
Resposta
Exercício Resolvido #2
Apostila de Primeira lei da termodinâmica - Universidade Federal de São Paulo
Um cilindro contém ar a e . Ele é aberto e deixado esvaziar até que sua pressão interna atinge . Qual será a temperatura ao final do processo? Assuma que não há troca de calor entre o cilindro e o ambiente. Dados: e
Passo 1
Fala aí! Partiu arrasar nesse assunto? Vamos lá!
Vamos começar anotando todos os dados do nosso enunciado, beleza?
Temos o seguinte:
Mas peraí! Esquecemos de uma informação importantíssima!
O enunciado disse pra gente assumir que Não existe troca de calor entre o cilindro e o ambiente! E o que isso significa? Que esse nosso processo é adiabático!

Em outras palavras… Nosso calor é zero:
Aaaahhhh simm!!
Passo 2
O enunciado pede a temperatura final do processo, e isso a gente sabe calcular com a equação do calor:
Opa! Para tudo! Se o nosso calor é zero, então nossa variação de temperatura tem que ser zero também, né?
E sendo a variação zero significa que:
Já temos nossa resposta então!
Mas vamos conferir?
Passo 3
Conferindo a observação que fizemos no passo anterior, vamos lá:
Olha aí! Confirmamos nossa hipótese!
Show! Arrasamos!!
Resposta
Exercício Resolvido #3
Apostila de Primeira lei da termodinâmica - Universidade da Beira Interior
A quantidade de energia transferida como calor para um sistema é de e a quantidade de energia transferida pelo sistema para o exterior através da realização de trabalho é . Calcule a variação de energia interna do sistema.
Passo 1
Fala aí! Vamos resolver essa questãozinha? Vamos sim!
Começando anotando todos os dados do nosso enunciado, tranquilo?
Temos o seguinte:
Mas peraí! Que sinal negativo é esse aí no trabalho?
![]()
O enunciado disse pra gente que o trabalho é transferido pelo sistema para o exterior, então ele é negativo, sacou?
Passo 2
Agora podemos calcular a variação de energia interna que o exercício pediu:
Show! Conseguimos!
Resposta
Exercício Resolvido #4
Lista sobre calor e trabalho - Instituto Federal do Rio Grande do Norte
Calcule a quantidade de calor necessária para fazer de água sair de até a sua temperatura de ebulição de . Dado: .
Passo 1
Fala aí! Vamos resolver essa questão? Vamos lá!
Começando anotando todos os dados do nosso enunciado, tranquilo?
Temos o seguinte:
Agora vamos para as continhas!
Passo 2
Agora podemos calcular a quantidade de calor necessária que o exercício pediu:
ou
Show! Conseguimos!
Resposta
Exercício Resolvido #5
Apostila de Primeira lei da termodinâmica - Universidade Federal de São Paulo
Um tanque rígido com volume de , contém nitrogênio () a e . O tanque é, então, resfriado até que a temperatura atinja . Determine o trabalho e o calor para esse processo.
Passo 1
Fala aí! Partiu arrasar nesse assunto? Vamos lá!
Vamos começar anotando todos os dados do nosso enunciado, beleza?
Temos o seguinte:
O enunciado ta pedindo pra gente o calor () e o trabalho (), podemos achar eles assim:
Vamos lá então!
Passo 2
Começando pelo calor, precisamos antes de tudo pegar o dado de calor específico que já é tabelado e encontrar a massa do nitrogênio, beleza?
Agora para encontrar a massa dele, vamos usar uma relação já conhecida entre a gente:
Nós temos o volume e podemos encontrar a densidade já tabelada:
Vamos nessa então:
Passo 3
Agora nós podemos calcular o calor! Vamos então:
Show! Arrasamos!!
E o trabalho será:
Maaaas, a gente ta falando de um gás dentro de um tanque rígido, certo?! Então não tem alteração de volume, logo:
Beleza! Conseguimos!
Resposta
Exercício Resolvido #6
Adaptado de Universidade Federal dos Pampas - Físico-Química III - Professor Márcio Marques
Determine qual deve ser, aproximadamente, a tensão superficial da água para que uma lâmina de barbear não flutue nela.
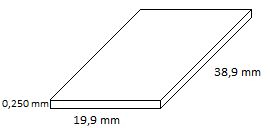
Dados:
Passo 1
Bom, essa questão aí é mais ou menos teórica… Vamos começar pensando o seguinte, para a lâmina de barbear afundar na água é preciso que:
Isso quer dizer que o trabalho da força peso, que foi dada, tem que ser maior que o trabalho da tensão superficial da água… Beleza! Agora vamos achar a tensão superficial que permite que essa lâmina afunde!
Vamos começar encontrando o trabalho realizado pela força peso, ok? Sendo a equação de trabalho definida por:
Vamos ter:
ou
Passo 2
Agora a gente precisa usar a relação que fizemos lá no início e encontrar a tensão superficial, ok? Vamos nessa!
Usando a definição inicial de tensão superficial, sabemos que:
Então vamos ter:
Opa! Show! Então se a tensão superficial da água for menor que a lâmina vai afundar.