Teoria
Fala aí! Bora conversar sobre Gases Ideais?!
O que é um Gás Ideal?
O gás ideal ou gás perfeito considera que não existe interação, atrativa ou repulsiva entre as moléculas e as as colisões entre as partículas são perfeitamente elástica, isso é, a sua energia cinética é constante.
Esse gás não existe na realidade, mas podemos considerar que um gás em baixas pressões, onde a interação entre moléculas gasosas não é muito grande, tem um comportamento similar a do gás ideal!
Nesse caso usamos a Lei dos Gases Ideais! 😉
📢 Clique para ver mais:
Lei dos Gases Ideais
A lei dos gases ideais tem essa carinha aqui:
Onde:
é a pressão; é o volume ocupado pelo gás; é o número de mols; é a temperatura; é a constante dos gases ideais, o seu valor depende das unidades que você esta utilizando as mais comuns são e .
O gás ideal é um gás que obedece à essa equação sob todas as condições.
A lei dos gases ideais veio da veio a Lei de Boyle, onde através de um experimento ele observou o seguinte comportamento:
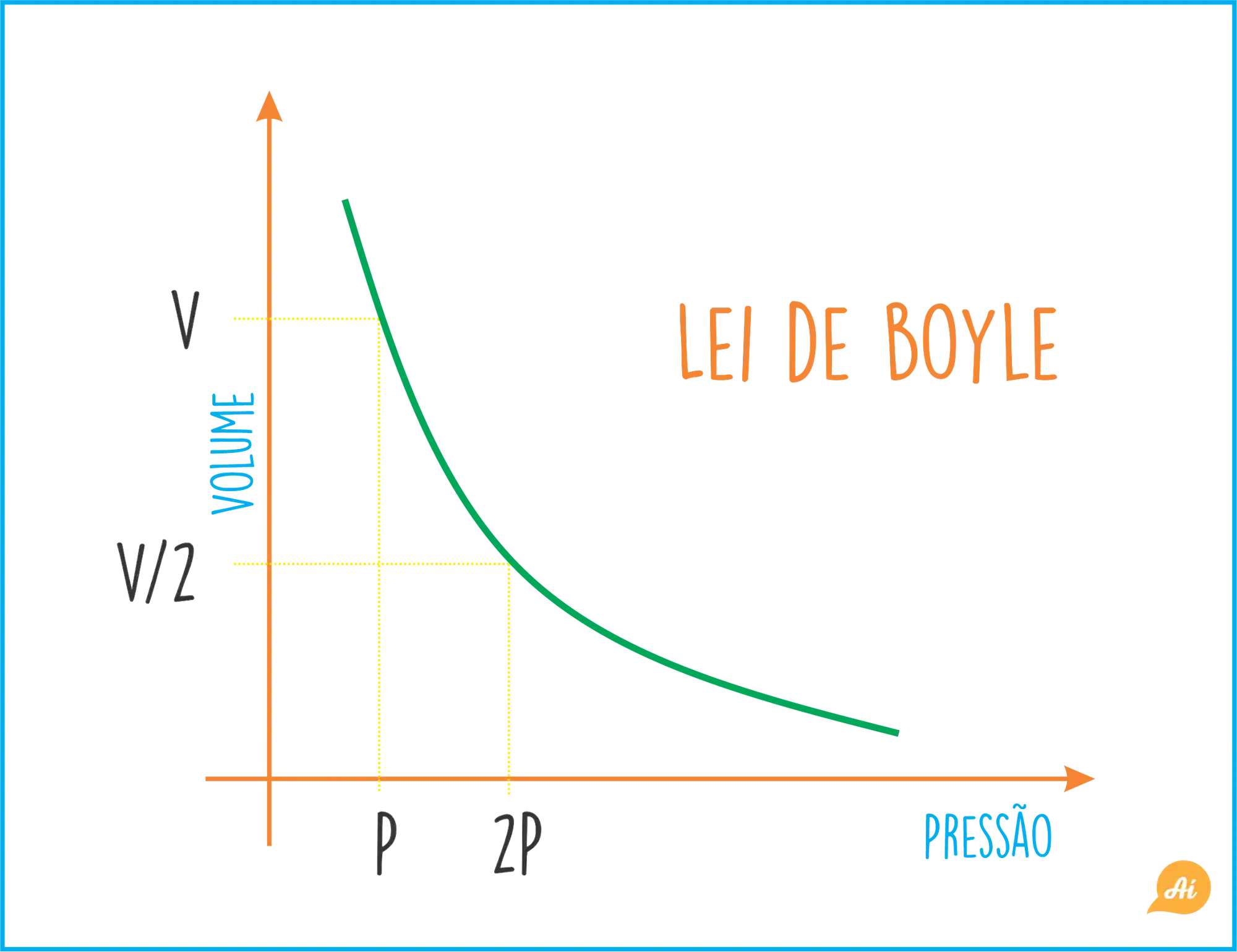
Quando estamos trabalhando com um processo isotérmico (temperatura constante), a pressão e o volume se comportam como mostra o gráfico.
Daí veio a equação:
Um tempo depois, veio a Lei de Charles, onde dessa vez a pressão foi mantida constante, enquanto variava a temperatura e o volume, e o resultado foi o seguinte:
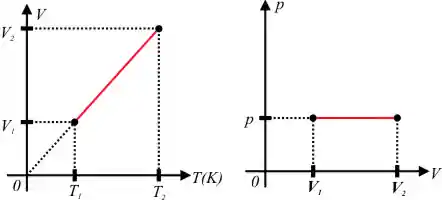
E a interpretação desses resultados nos trazem outra equação:
E vendo tudo isso Clapeyron, resolveu juntar essas informações e obteve a lei dos gases ideais ou equação de Clapeyron!
Essa equação é fruto de anos de estudos e observações experimentais, e pode ter certeza que você vai usar mais ela do que você imagina 🤣🤣🤣
Para que serve a Lei dos Gases Ideais?
A lei dos gases ideais é bem útil para descobrirmos parâmetros de um gás, como a pressão ou a temperatura.
Mas mais do que isso, ela nos permite calcular o comportamento de um gás com a mudança de um dos parâmetros.
Supondo que temos uma primeira situação, com pressão, temperatura e volume específicos:
Em seguida, fazemos uma expansão nesse gás, mudando o volume e a pressão, por exemplo, e configurando uma segunda situação:
Se isolarmos o
Logo:
Uma equação chamada lei combinada dos gases.
Gases na CNTP
Nas mesmas condições de temperatura e pressão, um mol de gás ocupa o mesmo volume, independente da sua identidade química.
Ou seja, tanto faz se o gás for
Daí surgiu o volume molar de um gás nas CNTP, as Condições Normais de Temperatura e Pressão,
Agora vamos praticar com exercícios?
Gases na CNTP
Exercícios Resolvidos
Exercício Resolvido #1
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp164-Exercício 4.17
Determine a pressão final quando:
a) de criptônio sob são transferidos para um recipiente de ;
b) de , sob , são comprimidos até .
Considere a temperatura constante e os gases ideais.
Passo 1
Para resolver esse problema vamos aplicar a lei combinada dos gases ideais, já que temos duas situações diferentes em que o número de mol do gás não muda:
Além de usar o fato de que os gases, por natureza, ocupam o volume do recipiente que se encontram.
a) Nessa letra temos de criptônio, logo
Como não houve mudança de temperatura, , então podemos multiplicar a fórmula por dos dois lados da equação.
Aplicando na fórmula:
Passo 2
b) de , sob 643 Torr, são comprimidos até .
Analisando os dados que o problema dá:
Assim, substituindo na lei combinada dos gases ideais:
Resposta
a)
b)
Exercício Resolvido #2
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp164-Exercício 4.19
Uma lata de aerossol de 250 ml em e 1,10 atm foi lançada em um incinerador. Quando a lata alcançou , ela explodiu. Qual era a pressão na lata no momento da explosão, imaginando que a pressão era a maior possível nesse momento?
Passo 1
Beleza, vamos tentar visualizar o que que está acontecendo nessa situação!
Uma lata de aerossol foi colocada num incinerador, ou seja, a temperatura dessa lata vai aumentar com o calor. Como a temperatura está aumentando, o volume dos gases dentro da lata vai expandindo, fazendo com que a pressão da lata aumente também, até que chegue num ponto que ela exploda.
Agora vamos pensar... o numero de mol dos gases dentro da lata não muda, já que não estamos tirando nem botando nada.
Assim, vamos usar a lei combinada dos gases ideais:
E com isso conseguimos encontrar a pressão da lata no momento da explosão.
Passo 2
Sabemos que na primeira situação as condições eram:
Já na segunda situação (a antes da explosão), não alteramos o volume da lata (logo ) e a temperatura é de
Substituindo na fórmula, chegamos então que:
Resposta
A pressão na lata era .
Exercício Resolvido #3
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp165-Exercício 4.27
Foi-lhe dito que de xenônio exercem a pressão de em .
a) Que volume a amostra ocupa sob e ?
b) Que pressão ela exerceria se fosse transferida para um frasco de em
c) Calcule a temperatura necessária para o xenônio exercer a pressão de nesse frasco.
Passo 1
a) Para essa questão, vamos usar a lei combinada dos gases ideais:
As condições iniciais o enunciado nos dá:
Nesse caso,
Substituindo na fórmula...
Obs importante: Quando a temperatura for negativa, como os , sempre é melhor trabalhar em Kelvin! Como o é o zero absoluto, ou seja, não existe temperatura negativa em K, sempre que houver uma temperatura negativa no exercício, passe ela pra Kelvin!!!
Passo 2
b) Mais uma aplicação da lei combinada dos gases ideais, mas agora as condições finais mudaram:
Aplicando na fórmula...
Passo 3
c) Novamente, aplicação da lei combinada dos gases ideais, mas dessa vez a temperatura é a icógnita!
Nas novas condições,
O volume não muda já que o frasco é o mesmo!
Aplicando na fórmula...
Resposta
a) 11,8 ml
b) 0,969 atm
c) 199 K
Exercício Resolvido #4
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp165-Exercício 4.25
Uma amostra de gás metano, , foi aquecida lentamente na pressão constante de . O volume do gás foi medido em diferentes temperaturas e um gráfico de volume versus temperatura foi construído. A inclinação da reta foi . Qual era a massa do metano?
Passo 1
Essa questão é um pouco diferente mas vamos com calma que sai! Ahhaha
Vamos começar pela lei dos gases ideais, pra ver se de lá conseguimos tirar alguma coisa:
No caso do exercício, sabemos que são constantes, já que não estamos mudando a quantidade de metano e a pressão é constante 0,9bar.
Assim, temos:
Com as unidades ajustadas, vamos tirar as unidades pra ver o que sobra:
Que é a equação de uma reta x !
Passo 2
Agora que descobrimos a equação da reta que foi traçada no gráfico, só substituir a inclinação da reta que o gráfico achou pela inclinação da reta que achamos pela fórmula:
Como precisamos calcular a massa, vamos usar a massa molar do metano:
Resposta
0,0495 gramas.
Exercício Resolvido #5
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp165-Exercício 4.31
Uma amostra de de ar, originalmente em e , foi aquecida até . Depois, a pressão foi levada a e a amostra, aquecida até . Por fim, a pressão foi abaixada até . Qual é o volume final da amostra de ar?
Passo 1
Vamos com calma porque nessa questão foram muitos processos seguidos!
Como foram muitos processos em que não mudamos a quantidade de ar, ou seja, não alteramos o número de mol, vamos usar a lei combinada dos gases ideais:
O primeiro processo foi:
Que foi aquecida até
O enunciado não diz nada sobre a pressão, mas aí entra a malandragem: como ele só fala que a pressão foi elevada no próximo processo, vamos considerar a pressão constante nessa primeira mudança, e só calcular a variação de volume!
Então,
Substituindo na fórmula...
Passo 2
Agora, já temos novas condições iniciais para o próximo processo:
Com a pressão e a temperatura variando, temos as condições:
Aplicando na fórmula...
Passo 3
Ufa! Última transformação!
Novas condições ideais (calculadas no passo 2):
Nessa transformação também vamos usar a malandragem de pensar que, como o enunciado não fala nada sobre a temperatura, ela fica constante! Então:
Aplicando na fórmula:
Passo 4
E se a gente tentar fazer direto?
Pois é, chegamos ao mesmo resultado, pois só precisamos mesmo do estado inicial e do final do processo.
Resposta
18 litros
Exercício Resolvido #6
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp166-Exercício 4.63
Um recipiente de volume contém de e de em Calcule suas pressões parciais e a pressão total.
Passo 1
Opa, lembra que é o volume ocupado por de um gás ideal nas CNTP ( e )?
E tá vendo que aí a gente tem no total?
Algum palpite pra pressão total? Eu aposto que, se com a gente tem , com a gente vai ter de pressão.
E pras pressões parciais, como estamos tratando esses caras como gases ideais, não faz diferença quem é quem. Se o hidrogênio tem dos mols que estão ali dentro, acho que ele vai ser responsável por da pressão. E o nitrogênio por . Mas vamos calcular pra ver se vai ser isso mesmo.
Passo 2
Vamos começar calculando a pressão total desses gases!
Como em baixas pressões e temperaturas misturas de gases que não interagem entre si se comportam como um gás puro, podemos calcular a pressão total considerando que temos 3 mols de gás.
Passo 3
Para calcular as pressões parciais dos gases, precisamos primeiro calcular suas frações molares!
As frações molares são calculadas por:
Pela definição de pressão parcial, sabemos que:
Resposta
Exercício Resolvido #7
Peter Atkins & Loretta Jones. Princípios da Química, 5ª ed. Porto Alegre: Bookman, 2012, pp168-Exercício 4.65
Um balão de contém o gás nitrogênio, em , em . 0,10 mol de é adicionado ao balão e os gases se misturam. Em seguinda, uma torneira se abre para permitir a saída de de moléculas. Qual é a pressão parcial do oxigênio na mistura final?
Passo 1
Podemos calcular o número de mols inicial de através da lei dos gases ideais:
Como
Assim, quando adicionamos de , o .
As frações molares da mistura, nessas condições, eram:
Passo 2
Como os gases foram misturados, quando o gás escapa, as propriedades da mistura não se alteram, isso é: as frações molares continuam as mesmas! Isso porque o que saiu tem a mesma composição do que ficou ali dentro.
Mas quando de moléculas saem da mistura, o novo se torna .
A nova pressão, portanto, é:
Passo 3
Pela definição de pressão parcial, sabemos que:
Resposta
1,95 atm
Exercício Resolvido #8
Lista de exercícios FSQ 1001, UDESC.
Dois frascos A e B, conectados por uma válvula, contêm, respectivamente, oxigênio e nitrogênio, a . No estado inicial, apresentam os seguintes dados:

A válvula é aberta e os gases se misturam. Atingido o equilíbrio, calcular:
a) A pressão total da mistura gasosa;
b) A pressão parcial de cada gás;
c) A fração molar do na mistura.
Passo 1
a) Como os gases se misturam, o vai ser a soma dos mols de cada um dos gases.
Para calcular o e o , vamos usar a lei dos gases ideais:
Onde e são dados na tabela, é e é 0,082 atm.L/mol.K.
Para o
Para o
Quando eles se misturam, portanto,
Passo 2
Para calcular a nova pressão total, vamos usar de novo a lei dos gases ideais!
Passo 3
b) Para calcular a pressão parcial de cada gás, precisamos calcular suas frações molares, já que a definição de pressão parcial é dada por:
Para calcular as frações molares:
Daí já calculamos a letra c!
Passo 4
Agora é só aplicar as frações molares e a pressão total na fórmula de pressão parcial :
Resposta
a)
b)
c)