Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 4.1 - Ex. 118
Mostre que o parâmetro b de van der Walls está relacionado com o volume molar, Vmol, por b = 4NAVmol. Trate as moléculas como esferas de raio r, de modo que Vmol = ¾r3. A aproximação máxima permitida dos centros é 2r.
Passo 1
Um recipiente de volume V contém n mols de gás que possuí um certo volume conhecido como volume excluído b. O volume molar de uma esfera é dado pela seguinte equação:
Passo 2
Duas moléculas de gás fechadas, cada uma com raio r é mostrada da seguinte fórmula: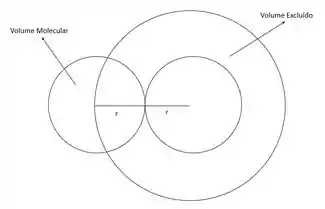 
Passo 3
O volume excluído para duas moléculas fechadas se dá:
Assim, o volume excluído para uma molécula de gás é:
Sendo, NA o Número de Avogadro
Resposta
Desse modo, percebemos que o volume excluído é 4 vezes o volume molar.
Exercícios de Livros Relacionados
76. Um composto usado para preparar cloreto de polivinila (PVC) tem a composição 38,4 % de C , 4,82 % de H e 56,8 % de C l , em massa. São necessários 7,73m i n para um determinado volume do composto
73. Uma amostra do gás argônio efunde por uma rolha porosa em 14 7s . Calcule o tempo necessário para a efusão do mesmo número de mols de (a) C O 2 , (b) C 2 H 4 , (c)H 2 , e (d) S O 2 nas mesma condi
Você sabe que 2,55 g de um hidrocarboneto gasoso enche um frasco de 3,00 L, em 0,950 atm e 82,0ºC. Escreva a fórmula de Lewis do hidrocarboneto.
Os espalhamentos de odores pelo ar ocorrem pela difusão de moléculas de gás. Alguém abriu um frasco contendo octanoato de etila na extremidade norte de uma sala de 5 m de comprimento e, simultaneament
Uma amostra sólida, finalmente pulverizada, de um óxido de ósmio (que funde em 40º°C e ferve em 130°C), cuja massa é 1,509 g, foi colocada em um cilindro dotado de um pistão móvel que pode se expandir