Desenvolva, de forma recursiva, uma função que recebe um inteiro e retorna que é dado por:
Passo 1
Eae, tranquilo?
Vamos analisar a função proposta chamando-a de . Essa função recebe um argumento inteiro e retorna um valor também inteiro, logo, podemos declarar e o seu argumento como .
![]()
Passo 2
Agora, vamos colocar as condições iniciais.
Pelo enunciado nós temos os valores de para e , então vamos colocar um condicional usando um pra quando assumir esses valores, a função retornar os valores que queremos:
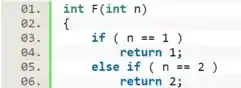
Passo 3
Por fim, temos que adicionar a recorrência para os casos diferentes de e .
Nesse caso, vamos usar a equação dada:
![]()
Resposta
