Os números de Catalan são definidos pela seguinte recursão
- , se
- , se
Alguns números desta sequência são:
Faça uma função recursiva que receba um número e retorne o N-ésimo número de Catalan.
Passo 1
Eai, tudo beleza?
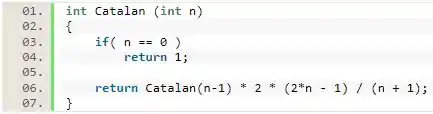
Nessa questão, nós temos que calcular os números da sequência de Catalan usando recursividade. Nesse caso, vamos iniciar a nossa função checando se o valor passado como parâmetro é igual a . Caso seja, vamos retornar , assim como o enunciado nos mostra funciona a sequência de Catalan. Esse será o caso que vai determinar o fim da recursividade.

Passo 2
Agora, vamos implementar a recursividade da sequência. Para isso, vamos fazer o nosso programa retornar . Dessa forma, vamos enviar sempre um número menor para a nossa função até que ele seja igual a e a recursividade seja encerrada.
![]()
Resposta