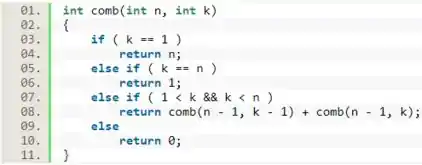
Escreva uma função recursiva que calcule o número de grupos distintos com pessoas que podem ser formados a partir de um conjunto de pessoas. A definição abaixo da função define as regras:
- , se
- , se
- , se
Caso sejam passados valores de e que não estejam especificados nas condições acima, faça a função retornar 0.
Passo 1
Eae, tudo tranquilo?
Nessa questão, estamos trabalhando com conceitos de combinatória e, por isso, devemos trabalhar com valores inteiros, pois a combinação de termos é melhor definida dessa forma. Nesse contexto, vamos declarar a função com os dois argumentos, e , e o retorno do tipo .
![]()
Passo 2
Agora, vamos colocar as condições iniciais que foram dadas. Caso , a função retorna e caso , ela retorna .

Passo 3
A seguir, vamos adicionar a relação de recorrência dessa função, que é dada por:
, se
![]()
Por fim, vamos acrescentar o caso de nenhuma das condições anteriores serem atendidas. Como foi definido no enunciado, caso isso aconteça, a função deve retornar .
![]()
Resposta