Seja a somatória abaixo. Faça uma função recursiva para realizar o cálculo.
Passo 1
Eai, tudo beleza?
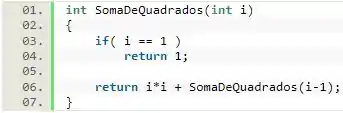
Nessa questão, nós temos que calcular uma soma de termos de forma recursiva. Uma boa maneira de fazermos isso, é fazermos uma função que recebe um valor e chama ela mesma, mas enviando um valor . Para que a função pare a recursividade, podemos fazer com que ela retorne , caso o valor enviado para ela seja , já que esse é o menor termo do somatório que está no enunciado.
Para começar o nosso código, vamos declarar a nossa função :
![]()
Passo 2
Dentro dessa função, a primeira coisa que vamos fazer é colocar o condicional para verificar se é igual a . Nesse caso, nós retornamos , encerrando a função.
![]()
Passo 3
Caso a função não esteja encerrada, ou seja, não é , vamos retornar + . Dessa forma, ao final da recursão, essa função retornará o somatório que queremos.
![]()
Resposta