Escreva uma função recursiva que calcule a soma dos primeiros cubos:
Chame essa função de . Crie também uma função que calcule essa soma de forma iterativa (usando laços de repetição, como e ) e chame-a de .
Passo 1
Eae, tudo tranquilo?
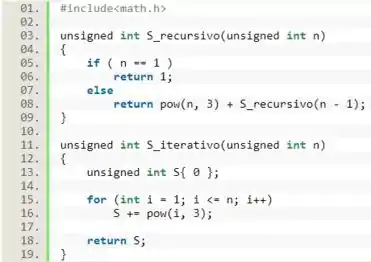
Vamos iniciar essa questão focando na função . Pra isso vamos relembrar que a recursividade é um mecanismo que permite uma função chamar a si mesma.
Para começarmos a trabalhar com essa função, precisamos determinar a recursão que será utilizada e os casos iniciais.
Para encontrarmos a nossa relação de recursividade, vamos escrever a função em função de :
Essa é a nossa relação de recursividade. Ela vai funcionar tipo um loop. Como, ao chamar um , será chamado sempre um valor menor de até que , precisamos estabelecer nosso caso inicial, que é o caso que a função não vai chamar a si mesma (). Esse vai ser o .
Com base nisso, vamos declarar essa função com ambos, retorno e parâmetro, como , pois só serão utilizados valores positivos nessa função.
![]()
Passo 2
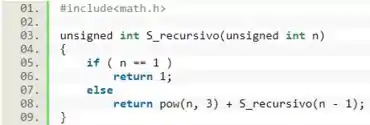
Já tendo definido o valor inicial para a nossa função de recursão, , vamos colocar isso no nosso código usando um condicional:

A seguir, vamos colocar a relação de recursão. E, para calcular o , vamos incluir a biblioteca e utilizar a função para calcular potências.
Passo 3
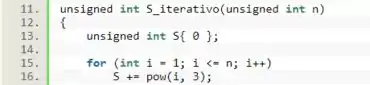
Agora, vamos focar na função . Como ele também irá trabalhar apenas com valores interos positivos, vamos declarar essa função e o seu parâmetro como .
![]()
A seguir, para calcularmos a soma dos cubos por meio de um laço de repetição, é necessário criar uma variável para acumular o valor dessa soma, que deverá ter valor inicial nulo. Vamos chamá-la de .
![]()
Vamos usar um laço de para que acumule o valor de cada cubo, e esse loop precisa fazer iterações. Então vamos definir a variável começando do e indo até o .
Por fim, basta retornarmos o valor de ao término do laço de .
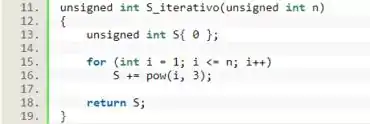
Resposta