A função de Ackermann é definida para valores inteiros e não negativos e da seguinte forma:
- , se
- , se e
- , se e
Faça uma função recursiva para implementá-la. Qual o valor de A(3,2)?
Passo 1
Eae, tudo tranquilo?
Para a função proposta nesse enunciado, teremos como parâmetros dois valores, e , ambos inteiros não negativos, assim como o valor a ser retornado pela função, então, podemos declarar esses valores como .
![]()
Passo 2
Vamos colocar os casos iniciais para a função de Ackermann. Temos o caso em que , no qual será retornado , e em que e , no qual será retornado
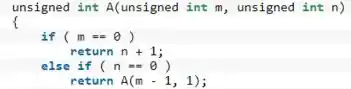
Repare que não é necessário especificar que no segundo caso, pois foi definido como , logo, temos e o caso de já foi considerado no primeiro condicional, ou seja, se a função não terminou no primeiro condicional, significa que é necessariamente maior que 0.
Passo 3
Agora, vamos acrescentar a recursividade dada por:
, se e
Similar ao caso anterior, não há necessidade de especificar as condições de e , pois são as únicas condições que sobraram para serem analisadas.
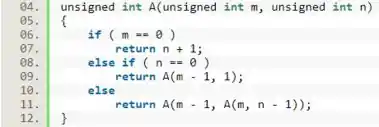
Perceba que é possível passar a própria função como um parâmetro, pois o retorno de foi declarado como do mesmo tipo dos parâmetros de .
Passo 4
Por fim, basta calcularmos o valor de . Para isso, vamos incluir a biblioteca e imprimir na tela tal valor.
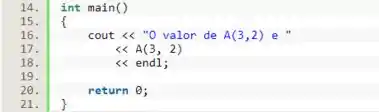
Resposta
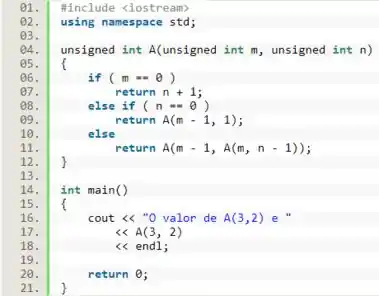
Para o valor de A(3,2), temos:
![]()