Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra dos Retângulos de Riemann

Ver Teoria
Exercício 51234

Enunciado

Calcular, pelo método dos retângulos de Riemann pela esquerda e pela direita a seguinte integral com n = 3 :

∫ 0 3 1 1 + x d x

Passo 1

Nosso primeiro passo será calcular o passo h com n = 3 :

h = b - a n = 3 - 0 3 = 1

Logo, nosso passo é h = 1 .

Passo 2

Agora, nós montamos uma tabelinha marota com pontos de 0 até 3 e calcule a função nesses pontos:

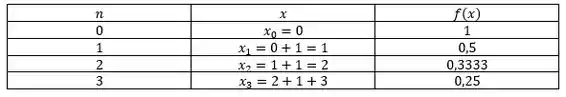
Agora, com esses falores podemos montar a integral pela esquerda e pela direira.

Passo 3

Os passos a esquerda, são os n primeiros valores a esquerda da curva. Ou seja, no intervalo de x 0 até x 2 :

I = h f ( x 0 + f ( x 1 ) + f ( x 2 ) ]

I = 1 1 + 0,5 + 0,333 = 1,833

Passo 4

Os passos a direita, são os n primeiros valores a direita da curva. Ou seja, no intervalo de x 1 até x 3 :

I = h [ f ( x 1 ) + f ( x 2 ) + f ( x 3 ) ]

I = 1 0,5 + 0,333 + 0,25 = 1 , 08 3

Resposta

Esquerda: I = 1,833

Direita: I = 1 , 0 83

Exercícios de Livros Relacionados

8. A regra dos Retângulos repetida é obtida quando aproximamos f ( x ) , em cada subintervalo, por um polinômio de interpolação de grau zero. Encontre a regra dos Retângulos bem como a expressão do er