Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra dos Retângulos de Riemann

Ver Teoria
Exercício 41235

Enunciado

Calcule a integral abaixo com n = 6 e compare com o valor real da integral dentro do intervalo dado:

∫ 0 1 7 x 5 d x = 1,1667

Passo 1

A primeira coisa que fazer é calcular o passo h :

h = 1 - 0 6 = 0,1667

Passo 2

Agora, calculamos os valores de pontos com o intervalo dado e as funções nesses pontos:

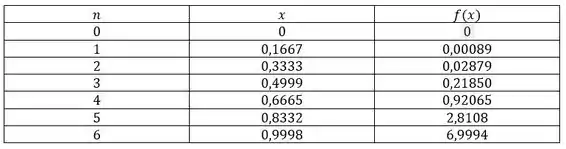
Passo 3

Faremos com o limite a esquerda, por convenção, e por isso não usaremos o valor de 6,9994.

I = h f ( x 0 + f ( x 1 ) + f ( x 2 ) + f ( x 3 ) + f ( x 4 ) + f ( x 5 ) ]

I = 0,1667 [ 0 + 0,00089 + 0,02879 + 0,2185 + 0,92065 + 2,8108 ]

I = 0,6633

Passo 4

Agora, fazemos a comparação do valor obtido com n = 6 e o valor real da função no intervalo.

Sendo a integral e seu valor real:

I R e a l = ∫ 0 1 7 x 5 d x = 1,1667

I R i e m a n n = 0,6633

E R = 1,1667 - 0,6633 1,1667 * 100 = 43 %

Resposta

I R i e m a n n = 0,6633

E R = 43 %

Exercícios de Livros Relacionados

8. A regra dos Retângulos repetida é obtida quando aproximamos f ( x ) , em cada subintervalo, por um polinômio de interpolação de grau zero. Encontre a regra dos Retângulos bem como a expressão do er