Um transformador de e possui reatância de dispersão do enrolamento de alta de , equanto que a correspondente do lado de BT é igual a . Determinar o circuito equivalente do transformador em pu considerando como bases as suas grandezas nominais.
Passo 1
O primeiro passo é escolher o valor base das grandezas. Escolhemos uma potência base para todo o sistema:
Agora, as tensões base:
Passo 2
Para calcular as impedâncias base, fazemos o seguinte:
Para o secundário:
Passo 3
Agora já conseguimos calcular o valor das impedâncias em pu:
Para o primário:
Para o secundário:
Passo 4
A impedância equivalente do circuito será, então:
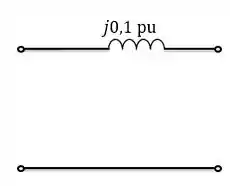
Resposta