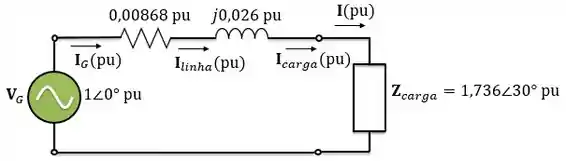
A figura abaixo mostra um sistema de potência simples. Esse sistema contém um gerador de ligado a um transformador elevador ideal 1:10, uma linha de transmissão, um transformador abaixador ideal 20:1 e uma carga. A impedância da linha de transmissão é e a impedância da carga é . Os valores de base escolhidos para esse sistema são e no gerador.
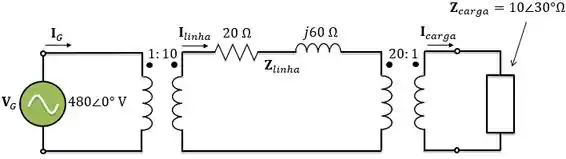
Encontre a tensão, a corrente, a impedância e a potência aparente, todos de base, em cada ponto do sistema de potência.
Converta esse sistema para seu circuito equivalente por unidade.
Passo 1
Como estamos trabalhando com pu, temos que encontrar o valor base das grandezas. Vamos dividir esse sistema em três regiões e determinar as grandezas base de cada região.
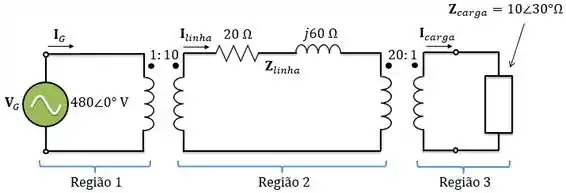
Para região 1 (gerador) o enunciado disse os valores de base escolhidos para esse sistema são e . Então,
Com esses valores bases a gente já consegue determinar os valores base para a impedância e corrente da região 1.
Passo 2
Para região 2, a potência base é a mesma, já que a gente escolhe uma para todo o circuito.
Como a relação de transformação do transformador 1 é 1:10,
A tensão base na região 2 tem que respeitar essa relação de transformação.
Então, a corrente e impedância base dessa região são:
Passo 3
A relação de transformação do segundo transformador é 20:1,
Então, respeitando a relação de transformação, a tensão base na região 3 será:
Então, a corrente e impedância base dessa região são:
Passo 4
Agora que os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
Da região 1, temos a tensão por unidade do gerador:
Da região 2, calculamos a impedância por unidade da linha:
Já da região 3, calculamos a impedância da carga em pu:
Passo 5
Agora, vamos desenhar o circuito equivalente por unidade desse sistema.
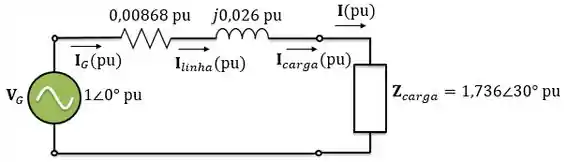
Observe que, em pu, o valor para a corrente é o mesmo em todos os trechos do sistema:
Resposta