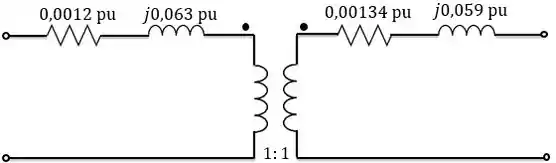
O circuito equivalente de um transformador de e está mostrado abaixo:
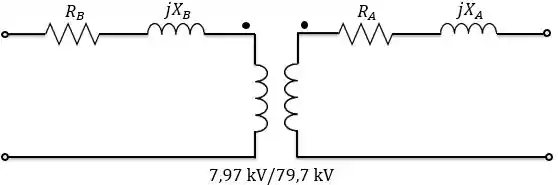
Os parâmetros do circuito equivalente são:
Converta os parâmetros do circuito equivalente para a forma por unidade usando as especificações nominais do transformador como base.
Passo 1
Como queremos trabalhar com pu, temos que encontrar o valor base das grandezas. Escolhendo a potência do transformador como potência base:
Agora escolhemos um valor de tensão base para cada trecho do sistema, ou seja, para cada lado do transformador. Escolhendo as tensões nominais do transformador:
Passo 2
Com esses valores bases a gente já consegue determinar os valores base para as impedâncias do primário e secundário.
Passo 3
Agora que os valores bases estão calculados, vamos passar nosso circuito inicial para pu. Para isso, pegamos o valor de cada grandeza que temos em nosso circuito e dividimos por seu respectivo valor base.
A impedância, em pu, para o lado de baixa (primário) será:
Já a impedância, em pu, para o lado de alta (secundário) será:
Passo 4
Então, em pu, temos o circuito equivalente abaixo:
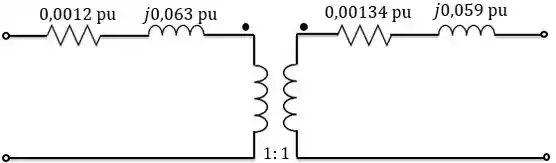
Como todo o circuito está em pu, não precisamos nos preocupar com a reflexão de impedâncias, já que, em pu, a relação de transformação é . Então, podemos omitir o transformador ideal e considerar o circuito equivalente abaixo para o transformador:
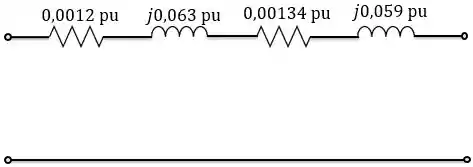
Resposta