Considere o “diagrama unifilar” de um sistema monofásico como mostrado abaixo, composto por um gerador G, um transformador elevador T1, uma linha de transmissão LT, um transformador abaixador T2 e uma carga puramente resistiva:
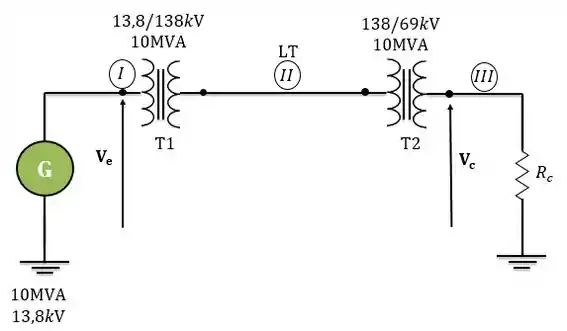
Os principais parâmetros desses equipamentos são dados abaixo:
G: gerador de
T1: transformador monofásico de impedância igual a referida para AT;
LT: Linha de transmissão com impedância de ;
T2: transformador monofásico de , , impedância igual a referida para BT;
Carga: resistência monofásica de
Condição de operação: a carga está sendo alimentada pelo transformador T2, com tensão de módulo igual a .
Determinar a tensão aplicada pelo gerador na entrada do sistema.
Passo 1
A primeira coisa que temos que fazer é determinar a potência base para todo o sistema:
Agora, precisamos encontrar as tensões base para cada trecho do circuito:
Passo 2
Da mesma forma, cada trecho terá sua impedância base:
Passo 3
Calculando as correntes base para cada trecho:
Passo 4
Agora já podemos calcular a impedâncias em pu. Lembrando que:
Para o transformador 1, como foi dito no enunciado que a impedância estava referida para o lado de AT, então significa que ela está no trecho :
Para a linha de transmissão, como ela está no trecho
Para o transformador 2, o enunciado diz que a impedância está referida para o lado de BT, que se encontra no trecho
Para a carga, que está no trecho :
Passo 5
Estamos quase terminando! Precisamos, agora, calcular a tensão da carga em pu, que está no trecho :
Adotaremos a tensão na carga como estando na referência:
A corrente na carga, em , será:
Então, o circuito em pu fica assim:
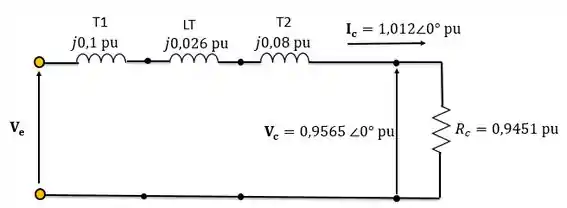
Passo 6
Como estamos interessados em determinar a tensão , utilizamos a Lei das Tensões de Kircchoff no circuito acima:
Passo 7
Finalmente, a tensão de entrada em volts, será: