Um transformador de e tem uma impedância em série equivalente de por unidade. Calcule a impedância em série equivalente em ohms referida ao lado de baixa e referida ao lado de alta tensão.
Passo 1
Em pu o valor da impedância equivalente do transformador, calculada por qualquer um dos lados, é único. Logo, temos o circuito equivalente abaixo para o transformador:
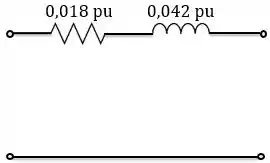
Passo 2
Como estamos trabalhando com pu, temos que encontrar o valor base das grandezas. Quando temos apenas um transformador sempre escolhemos a potência do transformador como potência base.
Agora escolhemos um valor de tensão base para cada trecho do sistema, ou seja, para cada lado do transformador. Sempre procuramos escolher as tensões nominais do transformador!
Passo 3
Com esses valores bases a gente já consegue determinar os valores base para as impedâncias do primário e secundário.
Passo 4
Agora, precisamos encontrar as impedâncias referidas para o primário e secundário em ohms. Para isso, temos que multiplicar o valor em pu pelo valor base:
A impedância referida para o lado de baixa (primário) será:
Passo 5
Já a impedância referida para o lado de alta (secundário) será: