Butano gasoso a e a é completamente queimado em regime permanente com de excesso de ar a e a . Determine a temperatura adiabádica de chama do produto!
Passo 1
Faaala, pessoal! Para entender melhor o que o exercício pede, temos que determinar os reagentes e produtos dessa combustão. O enunciado diz que reage com o e o do ar. Logo, os reagentes são , e . Além disso, o enunciado diz que a combustão é completa e com excesso de ar. Logo, , , e são os produtos da combustão!
onde , , , e são os coeficientes estequiométricos da equação de combustão.
Esses coeficientes são as vazões molares de cada substância. Como esse é um exercício pra achar a temperatura adiabática de chama , nós escrevemos a equação para de . Pra achar a temperatura , temos que descobrir a entalpia total dos produtos abaixo!
, , e são as vazões molares de , , e . , , e são as entalpias específicas em base molar de , , e .
O problema é: como podemos descobrir a soma das entalpias, se nós não sabemos quanto vale a temperatura dos produtos?

Nós podemos calcular isso, lembrando que, quando os produtos estão a temperatura adiabática de chama, eles mantiveram toda a entalpia dos reagentes na entalpia dos produtos! Em outras palavras, a soma das entalpias dos produtos é igual à soma das entalpias dos reagentes .
Como temos as temperaturas e pressões dos reagentes, podemos calcular a soma das entalpias dos reagentes que é igual à soma das entalpias dos produtos.
Depois de saber de tudo isso, podemos começar o exercício!
Passo 2
A soma das entalpias dos reagentes é a soma das entalpias de , e como mostrado abaixo.
, e são as vazões molares de , e e . , e são as entalpias específicas em base molar de , e .
Como foi dito antes, vamos considerar que a vazão molar do vale , porque estamos interessados em determinar a temperatura adiabática de chama .
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes da combustão de sem excesso de ar abaixo!
onde , , e são os coeficientes estequiométricos da combustão sem excesso de ar.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Pelo balanço de hidrogênio , os de dos reagentes são iguais aos dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
Tá, achamos todos os coeficientes estequimétricos da equação de combustão sem excesso de ar! Mas como podemos achar as vazões molares a partir disso?
Usando a porcentagem de excesso de ar. Quando o exercício diz que a combustão é feita com de excesso de ar, ele quer dizer que o coeficiente vé igual a mais de !
As outras vazões molares restante serão encontradas através do balanço da equação de combustão com excesso de ar.
Mas isso fica pro próximo passo!
Passo 3
Pra achar as outras vazões molares e , vamos precisar achar os coeficientes estequiométricos restantes , , e . Esses coeficientes são encontrados, fazendo o balanço químico da equação de combustão.
Achamos pelo balanço de carbono . Em outras palavras, os de carbono dos reagentes devem ser iguais aos de dos produtos.
Além disso, o coeficiente é encontrado através do balanço de hidrogênio . Os de dos reagentes devem ser iguais aos de dos produtos.
Achamos o coeficiente por meio do balanço de . A equação desse balanço se encontra abaixo.
A vazão molar de é encontrada através da fórmula abaixo.
Uhuuul! Achamos as vazões molares! Agora só falta achar as entalpias pra calcular os somatórios!
Passo 4
As entalpias precisam ser encontradas pra gente poder encontrar os valores dos somatórios!
A entalpia das substâncias é a soma entre a entalpia de formação e a diferença de entalpia .
é a diferença entre a entalpia da substância e a entalpia que ela teria caso estivesse a . Como o se encontram a nessa combustão, o do vale zero. Logo a entalpia do é igual à entalpia de formação.
Pra encontrar as diferenças de entalpia e de e do ar, vamos usar as tabelas de diferenças de entalpia . Buscaremos nelas pra e a .
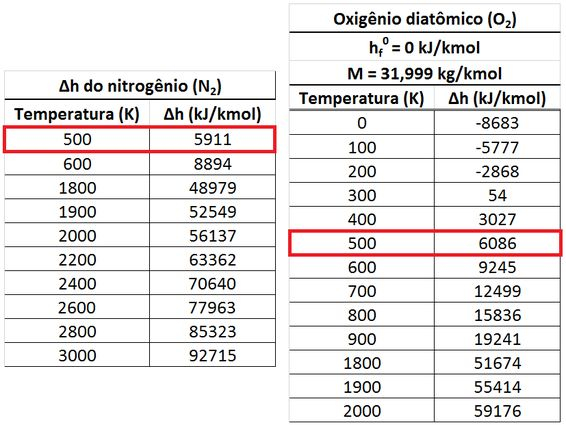
A entalpia de formação do e do valem zero, porque os dois são substâncias quimicamente mais estáveis. A entalpia de formação do pode ser encontrada na tabela de entalpias de formação.
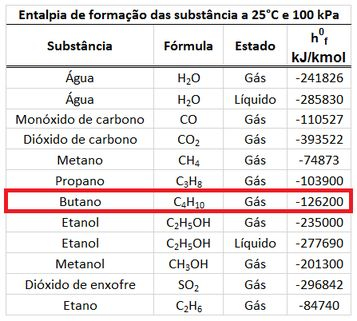
Com esses dados em mãos, podemos determinar os valores dos somatórios de entalpias!
Passo 5
O somatório das entalpias dos reagentes é:
Substituindo esse valor na equação do passo 1:
Eba! Achamos a entalpia total dos produtos! Mas como isso me ajuda a encontrar uma faixa de valore para a temperatura adiabática de chama?
Veremos isso no próximo passo!
Passo 6
Para a gente achar uma faixa de valores da temperatura adiabática de chama através da soma das entalpias dos produtos, precisamos separar as entalpias dos produtos (, , e ) nas entalpias de formação (, , e ) e nas diferenças de entalpia (, , e ).
O valor da entalpia específica está na tabela abaixo. Como a temperatura adiabática de chama é muito alta, a água vai estar no estado de vapor nos produtos. Por isso, usaremos a entalpia de formação do vapor d’água.
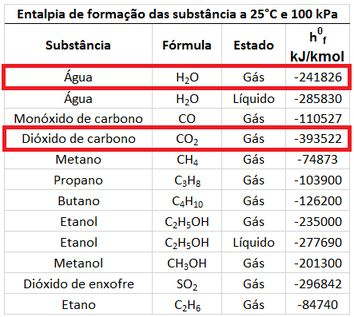
Os valores de , , e dependem da temperatura que ainda não foi descoberta. Substituindo os valores das entalpias de formação, encontramos o valor da soma entre as diferenças (, , e ).
Agora, a gente pode usar as tabelas de , , e para descobrir quanto vale a temperatura adiabática de chama dos produtos. Temos que ver qual valor de temperatura faz a soma de , , e ser igual a . Mas será que a gente vai ficar chutando valores de temperaturas até a gente acertar? Não tem estratégia melhor?
Passo 7
Temos uma estratégia melhor sim! Existe uma forma de descobrir uma faixa de valores possíveis para a temperatura adiabática de chama dos produtos. Conhecendo essa faixa, nós podemos testar alguns valores de temperatura de uma forma mais precisa. Ou seja, precisaremos de menos chutes e tentativas!

Para descobrir qual é essa faixa de valores, temos que dividir o valor da soma pela vazão molar total dos produtos . Dessa forma, a gente encontra uma média para os valores de .
Dividindo o valor da soma por , achamos a média de !
Usando as tabelas de , , e , podemos encontrar os valores de temperatura dos produtos para quando as entalpias , , e estão próximas de .
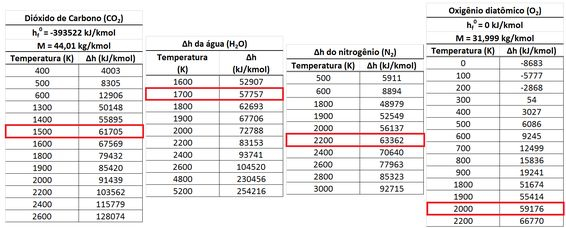
A imagem acima mostra que a temperatura dos produtos está entre e . Como existe mais nitrogênio nos produtos, a temperatura que queremos encontrar está mais próxima de . Ela só é um pouco menor que esse valor.
Veremos isso no próximo passo!
Passo 8
Como a temperatura adiabática de chama está mais perto de , vamos testar primeiro a temperatura de . Para testar essa temperatura, nós vamos calcular o valor do somatório , quando os produtos estão todos a . Se essa soma for menor que o valor , a temperatura é maior. Caso contrário, a temperatura é menor.
Os valores de , e para estão tabelados!
Nós encontramos um valor de somatório maior que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura menor que . Por conta disso, vamos testar agora um valor de temperatura um pouco menor que . Por exemplo, . Para esse valor, achamos:
Nós encontramos um valor de somatório menor que o valor real de . Isso quer dizer que, na realidade, os produtos da combustão tem temperatura maior que . Ou seja, a temperatura adiabática de chama dos produtos está entre e . Para encontrar a posição da temperatura dentro dessa faixa, interpolamos!
Esse resultado mostra que a temperatura adiabática de chama dos produtos da combustão vale . Note que, para interpolar, precisamos diminuir a faixa de temperaturas dos produtos. Inicialmente, faixa ia de a . Depois, a faixa ia de a . Isso foi importante, porque quanto menor a faixa, mais preciso é o resultado da interpolação.