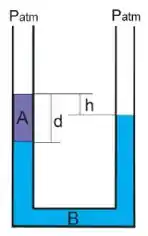
Dois líquidos e , possuem massa específica e . Estes fluidos são imiscíveis e estão em equilíbrio em um tubo em U, conforme ilustrado abaixo. O desnível entre as superfícies livres dos dois fluidos vale (em ):Dados:
Passo 1
Faaaala ai, belezinha? Vamos pra mais uma questão sobre o princípio de Stevin!
Lembra laa na teoria que o princípio de stevin diz pra gente que:
“A pressão em um mesmo fluido é igual em alturas iguais”
É isso que a gente vai fazer aqui, vamos pegar o ponto em que temos dois fluidos iguais que a gente saiba quais são as alturas!
Se liga nessa ajeitada que vamos fazer no nosso desenho!
Vamos escolher o ponto em que o líquido e se encontram, traçar uma reta horizontal e ver quais são as alturas!
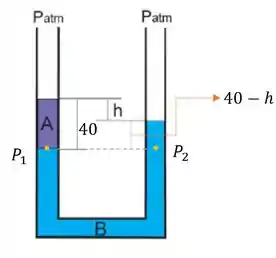
Aí sim! Podemos aplicar o Teorema de Stevin nessa altura!
Passo 2
Show agora que a gente entende melhor o que tá acontecendo vamos partir pra cima da nossa questão!
Pelo teorema de Stevin, temos que
Para o ponto , a pressão acima dele é
E a pressão de vale:
Para o ponto , temos que
E a pressão de vale:
Passo 3
Belezinha, agora vamos igualar as duas pressões!
Substituindo pelo que a gente achou, temos:
Podemos cortar os
como precisamos isolar o e temos aquele multiplicando geral, podemos passar ele para o outro lado dividindo
fazendo a divisão
passaremos o para o outro lado com sinal contrário
repare que ficamos com um , como faremos para consertar isso? Simples, só trocar o sinal de todo mundo! (é a mesma coisa que multiplicar todo mundo por )
Uhul! Achamos a resposta