O tubo de plástico da figura abaixo tem uma seção reta de . Introduz-se água no tubo até que o lado mais curto (de comprimento ) fique cheio. Em seguida, o lado menor é fechado e mais água é despejada no lado maior. Se a tampa do lado menor é arrancada quando a força a que está submetida excede , que altura da coluna de água do lado maior deixa a tampa na iminência de ser arrancada?
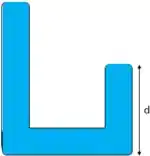
OBS.: use
Passo 1
Faaaala aí! Vambora pra mais um exercício para ficar fera no Princípio de Stevin!
Bom, de acordo com o Princípio de Stevin, temos que as pressões nos pontos e serão iguais:
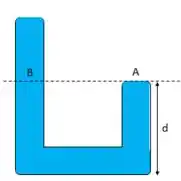
E podemos relacionar a pressão no ponto com a equação:
Onde será a altura da coluna de água acima desse ponto.
Passo 2
Bom, na situação descrita, nós vamos ter uma coluna d’água exercendo uma pressão no lado mais curto, para arrancar a tampa, logo, temos umas força associada a essa pressão.
E o enunciado diz que a força na iminência da tampa ser arrancada vale e que o tubo de plástico tem uma seção reta de . Para passar para vamos multiplicar por e isso vai nos dar.
A pressão e a força vão se relacionar por:
Agora, usando as duas equações encontradas:
Igualando os dois valores de , temos
Agora vamos substituir os valores de e
Para encontrar o precisamos passar o para o outro lado dividindo
Podemos cortar os e multiplicar por
Passo 3
Calma calma, ainda não terminou: esse valor de é a altura a partir do ponto B, lembra? Então, nossa verdadeira altura (do chão) vale:
Agora sim hehe acabamos a questão.
Resposta
A altura da coluna de água vale .